Обрабатывая наблюдения Марса, выполнявшиеся в течение 16 лет Тихо Браге, немецкий математик Иоганн Кеплер пытался установить истинную форму орбиты планеты, чтобы избежать расхождения между теоретически предвычисленными и наблюдаемыми ее положениями. На подбор кривой, которая описывала бы орбиту планеты с максимальной точностью, у него ушло почти 10 лет. В результате многолетней работы Кеплера появились три основные закона движения планет, которые носят его имя.

1-й закон Кеплера

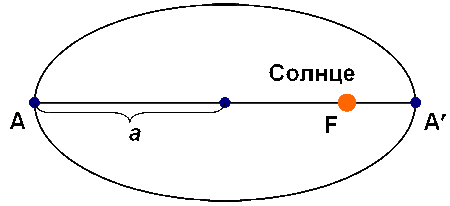
Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце (рис. 5.4).

Рис. 5.4. Орбита планеты – эллипс

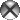
Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов F₁ и F₂) есть величина постоянная и равная длине большой оси: r₁ + r₂ = |AA′| = 2a.

Форму эллипса, степень его отличия от окружности характеризует эксцентриситет e = c/a, где с – расстояние от центра эллипса до его фокуса; а – большая полуось. Если e = 0, то эллипс превращается в окружность. Ближайшую к Солнцу точку орбиты (A′) называют перигелием, а наиболее удаленную (A) – афелием.

Учитывая закон всемирного тяготения, первый закон Кеплера можно сформулировать иначе: под действием силы тяжести одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе.