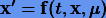 при условии x(0) = x0. Здесь x — искомое решение; t — независимая переменная, а
при условии x(0) = x0. Здесь x — искомое решение; t — независимая переменная, а 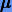 — некоторый малый параметр, причем такой, что при
— некоторый малый параметр, причем такой, что при 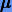 = 0 уравнение имеет аналитическое решение, выраженное через элементарные функции.
= 0 уравнение имеет аналитическое решение, выраженное через элементарные функции.Введение
Почти все важные для современной практики дифференциальные уравнения, описывающие физические явления, не интегрируются аналитически. Поэтому для их решения прибегают к приближенным методам интегрирования, которые условно делят на аналитические и численные. Рассмотрим их основные принципы на примере метода малого параметра и метода разложения в ряд Тейлора.
Пусть нам необходимо решить уравнение 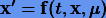 при условии x(0) = x0. Здесь x — искомое решение; t — независимая переменная, а
при условии x(0) = x0. Здесь x — искомое решение; t — независимая переменная, а 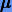 — некоторый малый параметр, причем такой, что при
— некоторый малый параметр, причем такой, что при 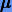 = 0 уравнение имеет аналитическое решение, выраженное через элементарные функции.
= 0 уравнение имеет аналитическое решение, выраженное через элементарные функции.
Именно это решение выбирается в качестве опорного 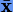 в аналитических методах, а приближенное решение представляется в виде усеченного ряда по степеням
в аналитических методах, а приближенное решение представляется в виде усеченного ряда по степеням 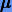 :
:
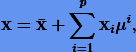
где p — порядок точности решения, а xi — неизвестные коэффициенты, которые определяются путем подстановки в дифференциальное уравнение степенного ряда и уравнивания коэффициентов при одинаковых степенях 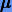 . При этом конструкция решения не зависит от начального условия, т.е. решение можно рассматривать как общее. Известно, что оно будет пригодным на временном интервале порядка
. При этом конструкция решения не зависит от начального условия, т.е. решение можно рассматривать как общее. Известно, что оно будет пригодным на временном интервале порядка 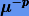 . Впрочем, эти замечательные особенности аналитического решения дискредитируются существенными недостатками, которые уже в настоящее время не могут быть не приняты во внимание.
. Впрочем, эти замечательные особенности аналитического решения дискредитируются существенными недостатками, которые уже в настоящее время не могут быть не приняты во внимание.

Обязательным условием для получения аналитического приближенного решения является наличие хорошего опорного, которое бы обеспечивало малость возмущений 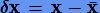 . Однако это не всегда возможно, как, например, в задачах астероидной динамики. Кроме того, для обеспечения достаточно высокой точности приближенного решения требуется большой порядок аппроксимации, что существенно усложняет решение. Именно эти недостатки становятся главной причиной, почему в современной практике все чаще прибегают к численной альтернативе в решении дифференциальных уравнений.
. Однако это не всегда возможно, как, например, в задачах астероидной динамики. Кроме того, для обеспечения достаточно высокой точности приближенного решения требуется большой порядок аппроксимации, что существенно усложняет решение. Именно эти недостатки становятся главной причиной, почему в современной практике все чаще прибегают к численной альтернативе в решении дифференциальных уравнений.
В методе разложения в ряд Тейлора в качестве опорного 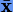 выступает начальное x0, а решение представляется в виде усеченного степенного ряда по t:
выступает начальное x0, а решение представляется в виде усеченного степенного ряда по t:
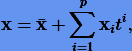
где p — порядок метода, а xi — коэффициенты ряда Тейлора. Несмотря на то, что численное решение пригодно лишь для малых t, эта трудность разрешается путем пошагового интегрирования: большой интервал времени делится на малые подынтервалы (шаги), на которых последовательно шаг за шагом определяются приближенные решения, при этом на каждом следующем шаге в качестве опорного выбирается решение предыдущего шага.
Отсюда главное достоинство численных методов состоит в том, что с их помощью почти всегда можно получить решение дифференциальных уравнений. Кроме того, методическая точность может быть повышена не только увеличением порядка аппроксимирующей формулы, но и уменьшением шага интегрирования. В связи с этим численное решение на шаге может быть довольно простым. Хотя необходимо заметить, что вследствие пошагового интегрирования компьютерная реализация каждого численного метода дает только частное решение.