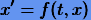
1. Терминология

Дифференциальное уравнение первого порядка — это уравнение вида

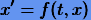(1.1)

с заданной функцией ƒ. Здесь штрих означает полную производную по времени.

Функция x = x(t) называется решением (1.1), если для всех t выполняется равенство

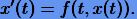(1.2)

На самом деле уравнение (1.1) имеет не одно, а целое семейство решений с одним свободным параметром. Этот параметр определяется единственным образом, если задано начальное условие

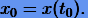(1.3)

Дифференциальное уравнение второго порядка имеет вид

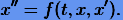(1.4)

Решение этого уравнения содержит уже два параметра, которые определяются из начального условия

(1.5)

Обычно при численном решении (1.5) вводят новые переменные , и это уравнение приводят к системе уравнений

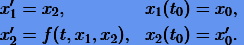(1.6)

Следует заметить, что подобным способом можно привести любую систему, состоящую из уравнений второго порядка, к системе уравнений первого порядка. Очевидно, (1.6) является частным случаем системы уравнений первого порядка общего вида

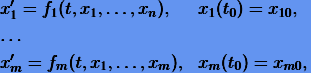(1.7)

или

(1.8)

где 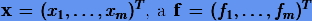. Дифференциальные уравнения (1.8) вместе со своими начальными условиями составляют задачу Коши.

В нашем курсе мы сосредоточим основное внимание именно на тех методах, которые были специально разработаны для численного интегрирования систем (1.8).

При этом мы будем полагать, что вектор-функция f удовлетворяет условию Липшица, т.е. для любых решений x₁ и x₂ справедливо неравенство

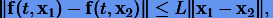(1.9)

где L — так называемая постоянная Липшица.