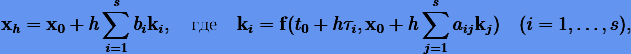
3.11.3. Формулы интегратора как одно из представлений неявного метода Рунге − Кутты

Пользуясь (3.49), (3.50) и (3.53), нетрудно показать, что решение (3.58) представимо в виде

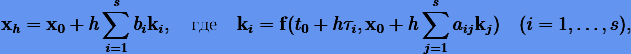
а коэффициенты 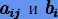— постоянные, зависящие только от . Таким образом, инте¬гратор Эверхарта фактически основан на видоизмененных формулах неявного метода Рунге − Кутты, который, кроме того, является коллокационным, что очевидно следует из (3.45)−(3.50). Поэтому порядок аппроксимирующей схемы интегратора можно повысить до p = 2s, если ее строить на узлах , являющихся корнями полинома Лежандра, т.е. если они удовлетворяют уравнению (3.44).

В оригинальной версии интегратора Эверхарта используется левое разбиение Гаусса − Радо и аппроксимирующая схема имеет меньший порядок p = 2s − 1. Несмотря на это, примечательность такого разбиения состоит в том, что оно не требует перевычислений коэффициента A₁ при решении нелинейных уравнений в схеме интегрирования, поскольку .