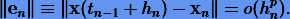
3.5. Оценка погрешности и выбор длины шага

Локальная погрешность метода — это погрешность на одном шаге. Как мы определили ранее, метод p-порядка имеет на каждом шаге локальную погрешность

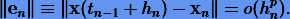
Это означает, что существует такая постоянная C, что для любых h_n справедливо неравенство

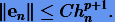(3.19)

Глобальной погрешностью называется погрешность численного решения после выполнения нескольких шагов.

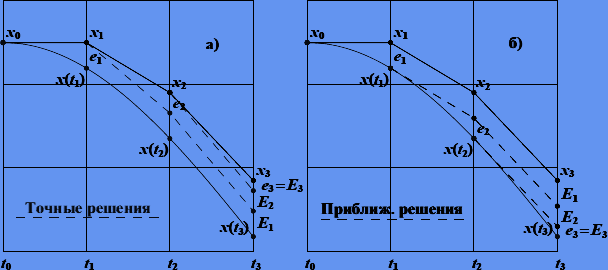
Рис. 3.1. Способы перенесения погрешностей

3.5.1. Оценка глобальной погрешности

Один из способов оценки глобальной погрешности является суммирование всех оценок для локальных погрешностей, перенесенных на конец интервала интегрирования. Погрешность на некотором n-м шаге переносится посредством выполнения оставшихся N − n шагов с использованием либо точных решений, либо приближенных (рис. 3.1).

В способе переноса погрешностей (рис. 3.1, б) на некотором n-м шаге рассматривают еще одно (ошибочное) решение z_n, которое отличается от решения x_n на локальную ошибку 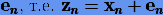. Для z_n схема интегрирования запишется как

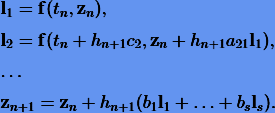
Тогда для норм разностей будем иметь

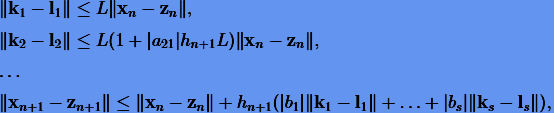(3.20)

где — постоянная Липшица для f.

Если ввести постоянную

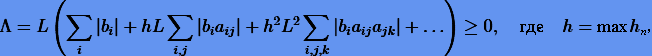
последнее неравенство (3.20) можно переписать как

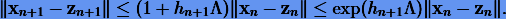
Отсюда оценка для перенесенной погрешности на n-м шаге будет

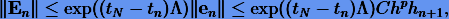
а оценка для глобальной погрешности

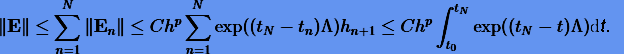
Наконец, получаем

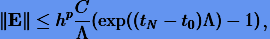(3.21)

или

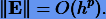
Отсюда следует, что все явные методы Рунге − Кутты сходящиеся, т.е.

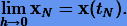
Оценку, подобную (3.21), для глобальной погрешности можно также получить и для неявных методов Рунге − Кутты, которые мы рассмотрим позже. Поэтому и все неявные методы — сходящиеся.