4. Экстраполяционные методы

Экстраполяционные методы основаны на том факте (который мы не будем доказывать), что глобальная погрешность численного решения порядка p допускает разложение в степенной ряд по h:

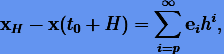(4.1)

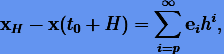
где 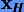— приближенное решение на отрезке H, полученное на равномерной сетке с шагом h.

Формула (4.1) представляет приближенное решение на фиксированном отрезке H как функцию 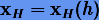. Для этой функции

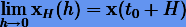
Теоретически это означает, что при достаточно малом шаге можно любым методом получить приближенное решение со сколь угодно высокой точностью. С практической точки зрения использование очень малых шагов не разумно, поскольку, во-первых, это увеличивает объем вычислений, что, во-вторых, сопряжено с большими ошибками округления. Тем не менее, используя идею экстраполяции, можно получить с высокой точностью предельное значение 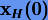, избегая при этом многочисленных вычислений.