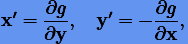
6. Геометрические методы
В последнее время в динамической астрономии возрос интерес к так называемым геометрическим численным методам интегрирования. Учитывая геометрические свойства дифференциальных уравнений, а точнее, их решений, эти методы позволяют качественно улучшить результаты численного интегрирования, в особенности, если оно выполняется на длительных (космогонических) интервалах времени.
Напомним сначала, что канонической системой уравнений называется система вида
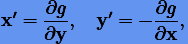 |
(6.1) |
где x и y — канонические m-мерные векторы, a g = g(x, y) — гамильтониан, который при этом является интегралом канонической системы: g(x, y) = const. Отметим важное для нас свойство канонической системы: преобразование временного сдвига
 |
(6.2) |
является симплектическим (каноническим). Действительно, ведь новые переменные также удовлетворяют системе (6.1).
Кроме того, заметим, что все рассматриваемые нами дифференциальные уравнения обратимы по времени. Это означает, что выполненные последовательно прямое и обратное интегрирования задачи Коши с одним и тем же шагом h дают ее начальные условия
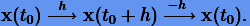 |
(6.3) |