6.1. Уравнения гармонического осциллятора
Рассмотрим уравнение гармонического осциллятора
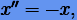 |
(6.4) |
которое представимо в виде системы уравнений первого порядка
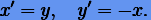 |
(6.5) |
Отметим важные свойства системы (6.5): 1) она имеет интеграл
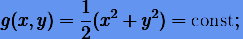 |
(6.6) |
2) система канонична с гамильтонианом g и, наконец, 3) она обратима по времени.
Таким образом, для интегрирования системы (6.5) целесообразно применять такие методы, которые бы учитывали названные свойства системы. Поскольку эти свойства тем или иным образом связаны с геометрией решений системы, то методы интегрирования, учитывающие хотя бы одно из них, обычно называют геометрическими.
Интересно заметить, что свойства 1)−3) характерны для многих дифференциальных уравнений небесной механики. В частности, уравнения кеплеровского движения (относительно центральной массы с гравитационным параметром 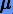 ) представимы в виде
) представимы в виде
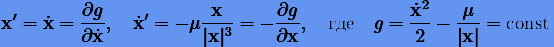
и они обратимы по времени.