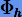 имеет порядок p = 2q а некоторые константы
имеет порядок p = 2q а некоторые константы 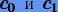 удовлетворяют условиям
удовлетворяют условиям6.4.4. Симплектические и симметрические методы высоких порядков
Составные методы. Интересный способ построения симплектических и симметрических методов высоких порядков — это последовательное использование на шаге простых схем интегрирования. Подобным образом мы уже получили методы Штермера − Верлета, а также симметрические методы средней точки и трапеций.
Особого внимания достойны составные методы Йошиды. Х. Йошида показал, что если симметрический метод 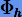 имеет порядок p = 2q а некоторые константы
имеет порядок p = 2q а некоторые константы 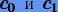 удовлетворяют условиям
удовлетворяют условиям
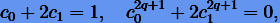 |
(6.22) |
то составной метод
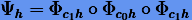 |
(6.23) |
является симметрическим и имеет порядок p =
2q + 2. Таким образом, это позволяет получить составные методы
любого четного порядка. Допустим, мы имеем симметрический
метод второго порядка 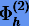 , например, средней точки или Штермера − Верлета. Тогда согласно (6.22) и (6.23) получаем метод четвертого порядка
, например, средней точки или Штермера − Верлета. Тогда согласно (6.22) и (6.23) получаем метод четвертого порядка
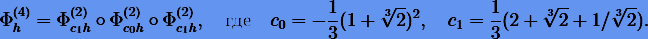
Применяя (6.23) 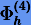 , получаем метод шестого порядка
, получаем метод шестого порядка 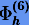 с соответствующими коэффициентами
с соответствующими коэффициентами 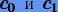 и т.д. Очевидно, если исходный метод
и т.д. Очевидно, если исходный метод 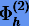 симплектический (например, Штермера − Верлета), то и составной метод, построенный на его основе, также будет симплектическим.
симплектический (например, Штермера − Верлета), то и составной метод, построенный на его основе, также будет симплектическим.
Заметим, что очередное повышение порядка по схеме (6.23) утраивает применение
исходного метода 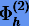 , так что в составном методе порядка p = 2q число использования исходного метода будет равно
, так что в составном методе порядка p = 2q число использования исходного метода будет равно 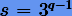 . Например, s = 27 уже при порядке p = 8. В связи с этим для методов высоких порядков возникает проблема уменьшения числа s при сохранении порядка. Разрешая эту проблему, У. Кахану и Р. Ли (1997) удалось получить составной симметрический метод восьмого порядка (отличный от метода Йошиды) с числом s = 17.
. Например, s = 27 уже при порядке p = 8. В связи с этим для методов высоких порядков возникает проблема уменьшения числа s при сохранении порядка. Разрешая эту проблему, У. Кахану и Р. Ли (1997) удалось получить составной симметрический метод восьмого порядка (отличный от метода Йошиды) с числом s = 17.
Отметим очевидные свойства составных методов вида
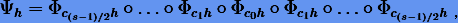
такие как: 1) методу 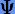 передаются свойства симметричности либо симплектичности метода Φ; 2) если метод Φ сохраняет какой-либо инвариант системы уравнений, то и составной метод
передаются свойства симметричности либо симплектичности метода Φ; 2) если метод Φ сохраняет какой-либо инвариант системы уравнений, то и составной метод  также будет сохранять этот инвариант.
также будет сохранять этот инвариант.
Методы Гаусса. В 1988 г. И.М. Санц − Серна и Ф.М. Ласани обнаружили, что если коэффициенты неявного метода Рунге − Кутты удовлетворяют условиям
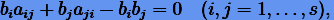 |
(6.24) |
то метод является симплектическим. Нетрудно убедиться, что согласно (6.24) среди одноэтапных методов Рунге − Кутты симплектическим будет только метод средней точки с коэффициентами 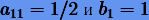 . В общем случае условиям (6.24), оказывается, удовлетворяют методы Гаусса − Лежандра (см. разд. 3.9), которые, кроме того, являются симметрическими.
. В общем случае условиям (6.24), оказывается, удовлетворяют методы Гаусса − Лежандра (см. разд. 3.9), которые, кроме того, являются симметрическими.
Многошаговые методы. Эффективными геометрическими методами высоких порядков среди многошаговых являются симметрические методы Куинлэна − Тремейна, которые применяются для интегрирования уравнений второго порядка 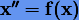 и имеют вид
и имеют вид
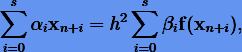
где 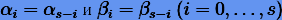 . Авторы получили методы вплоть до 14-го порядка и продемонстрировали их высокую эффективность на примере планетной задачи.
. Авторы получили методы вплоть до 14-го порядка и продемонстрировали их высокую эффективность на примере планетной задачи.