2.1 Аддитивные цветовые модели

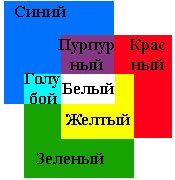
Аддитивный цвет получается путем соединения лучей света разных цветов. В основе получения аддитивного цвета лежат законы Грассмана, так как большинство цветов видимого спектра могут быть получены путем смешивания трех основных цветовых компонент (первичные цвета − красный (Red), зеленый (Green) и синий (Blue) или RGB (рис. 2.2)). При смешении основных цветов, например синего и красного, получается пурпурный (Magenta), при смешении зеленого и красного − желтый (Yellow), при смешении зеленого и синего − голубой (Сyan). При смешении всех трех цветовых компонентов получается белый цвет (White) (рис. 2.2). Голубой, пурпурный и желтый цвета называются вторичными цветами. Следует отметить, что первичные и вторичные цвета относятся к базовым цветам.

Базовыми цветами называют цвета, с помощью которых можно получить практически весь спектр видимых цветов.

Цветовая модель RGB используется для цветовоспроизведения, например воспроизведения цвета на экранах телевизоров и компьютеров, также аддитивные цвета нашли широкое применение в системах освещения, сканерах и цифровых аппаратах.

Рис. 2.2. Аддитивная цветовая модель

Математически цветовую модель RGB удобнее всего представлять в виде куба (рис. 2.3). В этом случае каждая его пространственная точка однозначно определяется значениями координат X, Y и Z. Если по оси X откладывать красную составляющую, по оси Y − зеленую, а по оси Z − синюю, то каждому цвету можно поставить в соответствие точку внутри куба.

При использовании этой модели любой цвет может быть представлен в цветовом пространстве с помощью вектора, описываемого уравнением: сС = rR + gG + bВ.

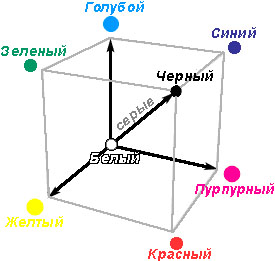
Рис. 2.3. Цветовая модель RGB

Уравнение идентично уравнению свободного вектора в пространстве, рассматриваемому в векторной алгебре. При этом направление вектора характеризует цветность, а его модуль выражает яркость [6].

На диагонали (ахроматической оси), соединяющей точки с координатами (R, G, В) = (0, 0, 0) и (R, G, В) = (255, 255, 255), расположены различные градации серого, для которых значения красной, зеленой и синей составляющих одинаковы. На рис. 2.4 приведен пример практической реализации RGB-модели в программе Corel PHOTO-PAINT.

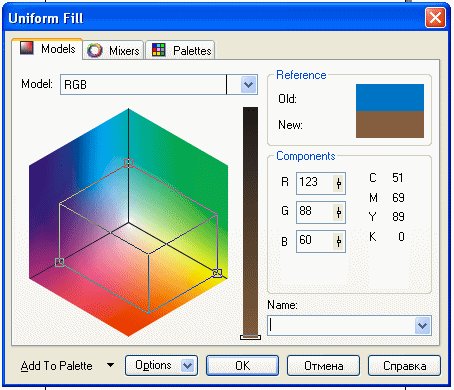
Рис. 2.4. RGB-модели в программе Corel PHOTO-PAINT