3.1 Цветовая система RGB МКО

Цветовая система RGB MKO является продолжением развития цветовой модели RGB. В данной системе учитываются свойства цветового зрения человека. По результатам экспериментов со смешением цветов были определены кривые сложения (рис. 3.1) линейно независимых цветов соответствующих монохроматическим излучениям с длинами волн 700,0 нм (красный), 546,1 нм (зелёный) и 435,8 нм (синий). При допущении отрицательных значений цветовой координаты уже все спектральные цвета можно выразить через выбранную тройку основных цветов.

В таких экспериментах выполняется зрительное уравнивание чистых спектральных цветов (т.е. цветов, соответствующих монохроматическому свету с различными длинами волн) со смесями 3 основных цветов.

При графическом построении зависимостей количеств основных цветов от длины волны получаются функции длины волны, называемые кривыми сложения цветов или просто кривыми сложения.

Система RGB МКО обладает рядом недостатков, основными из которых являются сложность расчетов и наличие отрицательных координат (рис. 3.1), что неизбежно в случае попытки воспроизведения всех цветов видимого спектра при использовании в качестве основных цветов компонентов RGB-модели.

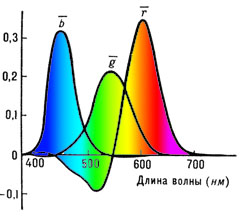
Рис. 3.1. Система RGB МКО. Распределение по спектру цветовых координат монохроматических излучений мощностью в 1 Вт

В настоящее время система RGB МКО в основном выполняет вспомогательную, а иногда контрольную функцию. Тем не менее именно эта система явилась основой цветовой системы XYZ.

Необходимость отрицательного компонента цвета

Как уже отмечалось, с помощью аддитивного синтеза невозможно создание всех цветов видимого спектра [6]. Например, для получения сине-зеленого цвета необходимо объединить потоки синего и зеленого цветов, но их сумма выглядит светлее, чем необходимый цвет. Если попытаться сделать его темнее с помощью красного, то получим еще более светлый результирующий цвет, так как световые энергии при аддитивном синтезе складываются. То есть мы можем добавлять красный только для получения более светлого образца. С точки зрения математики для получения нужного нам цвета необходимо вычесть красный цвет из суммы двух оставшихся базовых цветов, то есть добавить отрицательный компонент красного цвета (рис. 3.1):

С = gG + bВ − rR.

Однако физически это невозможно, так как отрицательной интенсивности света не существует.