5 Компьютерная геометрия

Математический аппарат, положенный в основу компьютерной графики, называют "компьютерная геометрия" [7, 14]. С помощью компьютерной геометрии мы можем изменять масштаб изображений, вращать последние, смещать и трансформировать для улучшения наглядности перспективного изображения. Все эти преобразования можно выполнить на основе математических методов.

В данном разделе мы рассмотрим виды проекций, трехмерные преобразования, алгоритмы растровой графики, алгоритмы удаления невидимых линий и ребер, модели расчета освещенности граней трехмерных объектов.

Для более подробного изучения темы "Компьютерная геометрия" можно обратиться к книгам, посвященным алгоритмам машинной графики [24, 25].

5.1 Проецирование трехмерных объектов

В общем случае проекции преобразуют точки, заданные в системе координат размерностью n, в системы координат размерностью меньше, чем n.

Для того чтобы увидеть на плоскости монитора трехмерное изображение, нужно уметь задать способ отображения трехмерных точек в двумерные. Способ перехода от трехмерных объектов к их изображениям на плоскости будем называть проекцией. Проекция трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проекционных лучей, называемых проекторами, проходящих через каждую точку объекта, пересекая картинную плоскость, образуя проекцию.

Виды проекций

Тип проецирования на плоскую, а не искривленную поверхность, где в качестве проекторов используются прямые, а не искривленные линии, называется плоской геометрической проекцией или просто проекцией. Плоские геометрические проекции делятся на два вида:

• центральные (перспективные);

• параллельные (аксонометрические).

Если центр проекции находится на конечном расстоянии от проекционной плоскости, то проекция − центральная (рис. 5.1). Если же центр проекции удален на бесконечность, то проекция − параллельная (рис. 5.2).

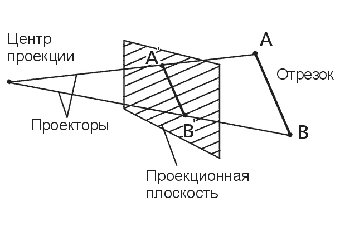
Рис. 5.1. Центральная проекция

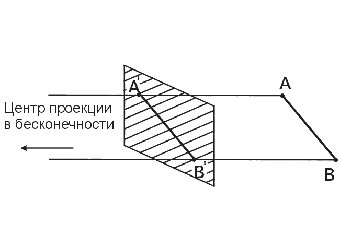
Рис. 5.2. Параллельная проекция

Полная классификация проекций приведена на рис. 5.3

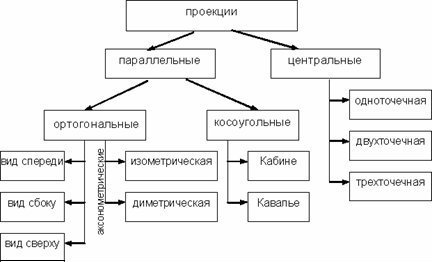
Рис. 5.3. Классификация проекций

Параллельные проекции делятся на два типа:

1) ортогональные (направление проецирования является нормалью к проекционной плоскости);

2) косоугольные (направление проецирования и нормаль к проекционной плоскости не совпадают).

При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются. В изометрической проекции нормаль к проекционной плоскости и направление проецирования составляет равные углы с каждой из осей системы координат.

Косоугольные (наклонные) проекции сочетают в себе свойства ортогональных проекций (видов спереди, сверху и сбоку) со свойствами аксонометрии. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерить углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Отметим, что нормаль к проекционной плоскости и направление проецирования не совпадают.

Двумя важными видами косоугольных проекций являются проекции:

Направление проецирования составляет с плоскостью угол 45^o. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т.е. отсутствует укорачивание.

Имеет направление проецирования, которое составляет с проекционной плоскостью угол = arctg(1/2) (~26,5^o). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют 1/2 их действительной длины. Проекции Кабине являются более реалистическими, чем проекции Кавалье, так как укорачивание с коэффициентом 1/2 больше согласуется с нашим визуальным опытом.

1) Кавалье (cavalier);

2) Кабине (cabinet).

Центральная проекция приводит к визуальному эффекту перспективного укорачивания, когда размер проекции объекта изменяется обратно пропорционально расстоянию от центра проекции до объекта. Центральная проекция любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будет сходиться в точке схода. Точек схода бесконечно много. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. В зависимости от того, сколько координатных осей пересекает проекционную плоскость, различают три вида проекций:

1. Одноточечная (рис. 5.4).

2. Двухточечная (широко применяется в архитектурном, инженерном и промышленном проектировании).

3. Трехточечная центральная (практически не используется).

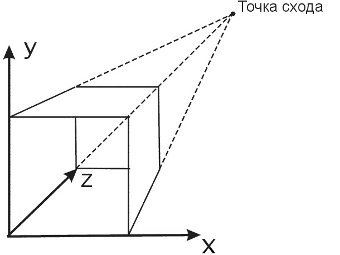
Рис. 5.4. Одноточечная проекция