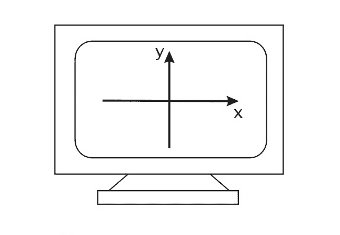
Рассмотрим более подробно центральную перспективную проекцию с математической точки зрения. Для получения формул центральной перспективной проекции расположим оси системы координат, проекционную плоскость и центр проекции, как показано на рис. 5.5.

Рис. 5.5. Расположение осей координат на экране
Будем имитировать на экране то, что как будто бы реально находится в пространстве за ним. Для этого будем использовать линейную аппроксимацию объектов в трехмерном пространстве с помощью отрезков прямых и плоских многоугольников. При этом отрезки прямых после перспективного преобразования переходят в отрезки прямых на проекционной плоскости (на монитор). Это важное свойство центральной перспективы позволяет производить вычисления только для конечных точек отрезков, а затем соединять проекции точек линиями уже на проекционной плоскости.
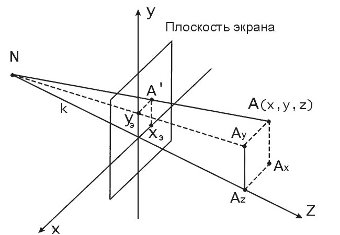
Рис. 5.6. Центральная перспективная проекция
Точка 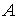 проецируется на экран как
проецируется на экран как 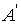 . Расстояние от наблюдателя до проекционной плоскости равно k, а наблюдатель находится в точке
. Расстояние от наблюдателя до проекционной плоскости равно k, а наблюдатель находится в точке 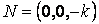 (рис. 5.6).
(рис. 5.6).
Необходимо определить координаты точки 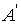 на экране. Обозначим их
на экране. Обозначим их 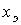 и
и 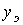 . Из подобия треугольников
. Из подобия треугольников 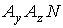 и
и 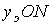 находим, что
находим, что
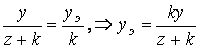 , тогда , тогда 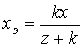 . . |
(1) |
Если точку наблюдения поместить в начало координат, а проекционную плоскость на расстояние 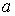 , как показано на рис. 5.7, то формулы для
, как показано на рис. 5.7, то формулы для 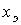 и
и 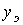 примут вид:
примут вид:
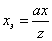 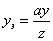 . . |
(2) |
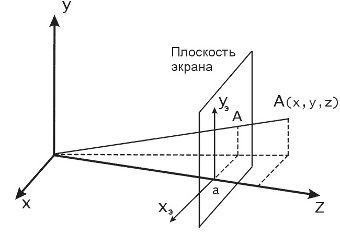
Рис. 5.7. Другой способ вычисления координат точек в центральной перспективной проекции
Формулы (1) более удобны при необходимости простым образом приближать или удалять наблюдателя от проекционной плоскости. Формулы (2) требуют меньше времени для вычислений за счет отсутствия операции сложения.