5.2 Трехмерное моделирование объектов

В настоящее время благодаря новейшим средствам, заложенным в микропроцессор, трехмерные объекты строятся на основе математического моделирования, а затем посредством специальных аппаратных и программных средств трехмерной графики происходит визуализация объектов на монитор компьютера.

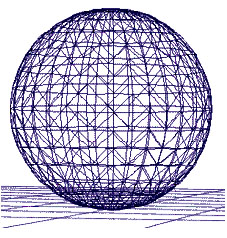
Традиционно для моделирования трехмерных объектов используются треугольники или многоугольники (например, проволочная модель сферы которая изображена на рис. 5.8). Затем выполняются модельные преобразования (перенос, вращение и изменение масштаба). Далее выбирается модель освещения и вычисляется освещенность объектов. Затем изменяются размеры треугольников в зависимости от положения точки наблюдения сцены.

Рис. 5.8. Проволочная модель сферы

Для усиления эффекта трехмерной глубины в моделях объектов удаляют невидимые линии, закрашивают и накладывают текстуру на треугольники, затем для устранения эффекта ступенчатости изображения применяют алгоритм сглаживания.

5.3 Трехмерные матричные преобразования

Однородные координаты − это координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же ненулевое число.

Рассмотрим трехмерную декартовую систему координат. Из курса геометрии известно, что точка в трехмерном пространстве описывается радиус-вектором r и координатами (x,y,z). Для реализации трехмерных преобразований с помощью матриц необходимо перейти к однородным координатам (x,y,z,1).

Тогда матрица трехмерного преобразования 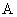(переноса, масштабирования, поворота) в общем виде будет следующей:

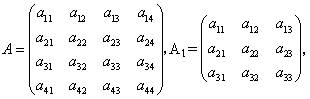
где матрица A₁ осуществляет линейное преобразование в виде изменения масштаба, сдвига и вращения, вектор (a₄₁,a₄₂,a₄₃) производит перенос объекта, а вектор-столбец (a₁₄,a₂₄,a₃₄)^T − преобразования в перспективе. Скалярный элемент a₄₄ выполняет общее изменение масштаба.

Матрица трехмерного переноса

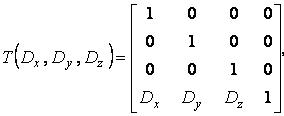
при этом

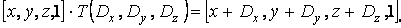
Операция масштабирования (частичная)

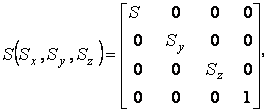
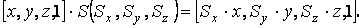
Трехмерный сдвиг

Недиагональные элементы матрицы A₁ осуществляют сдвиг в трех измерениях, т.е.

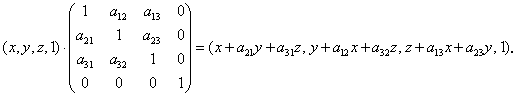
Трехмерное вращение

Матрица поворота вокруг оси Oz имеет вид:

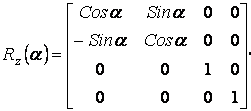
Матрица поворота вокруг оси Ox имеет вид:

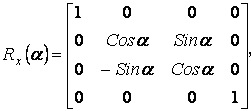
и вокруг оси Oy:

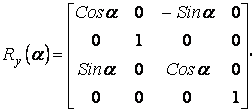
Обратные преобразования будут выражаться обратными матрицами. Для операции переноса надо лишь заменить знаки компонент вектора переноса на противоположные:

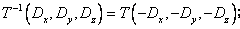
для операции масштабирования − на обратные значения:

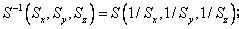
для поворота − выбором отрицательного угла поворота:

.

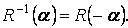Результатом нескольких последовательных поворотов будет матрица

Здесь верхняя матрица размером 3x3 является ортогональной.

Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и сдвига − нет.