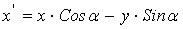5.4 Эффективность вычислений

Рассмотрим проблему ускорения вычислений в одной из самых трудоемких операций компьютерной графики − операции поворота точки относительно начала координат. Для выполнения этой операции необходимо произвести 4 операции умножения, 2 операции сложения, а также вычислить значения синуса и косинуса угла поворота:

,

.

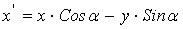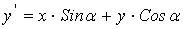Среди наиболее часто встречающихся способов ускорения операции поворота − отказ от вычисления синуса и косинуса угла во время выполнения программы и использование их заранее подсчитанных значений, которые занесены в специальную таблицу (табличный поворот).

Дополнительным способом ускорения операции поворота является уменьшение количества операций умножения. Таким способом является применение формулы О. Бьюнемана (3), в которой поворот точки вокруг начала координат производится за 3 операции умножения и 3 операции сложения.

Бьюнеман О. Многомерные преобразования Хартли // ТИИЭР. 1987. №2. С. 97-98.

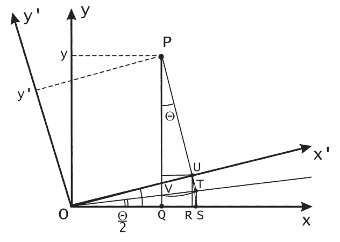
Рис. 5.9. Схема вывода формулы О. Бьюнемана

, , .

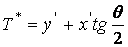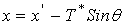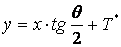(3)

5.5 Алгоритмы растровой графики

Растр − прямоугольная сетка точек, формирующих изображение на экране компьютера. Каждая точка растра характеризуется двумя параметрами: своим положением на экране и своим цветом.

В разделе 4.5.1 мы познакомились с понятием растр. Поскольку растровые изображения состоят из множества дискретных точек, то для работы с ними необходимы специальные алгоритмы. Рисование отрезка прямой линии − одна из простейших задач растровой графики. Смысл ее заключается в вычислении координат пикселов, находящихся вблизи непрерывных отрезков, лежащих на двумерной растровой сетке.

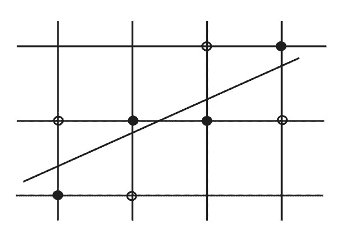
Рис. 5.10. Растеризация отрезка прямой линии

Простейшие пошаговые алгоритмы построения отрезка с помощью известного уравнения прямой y = kx + b имеют ряд недостатков, связанных с выполнением операций с вещественными числами и накоплением ошибок округления.

Эти недостатки устранены в следующем алгоритме Брезенхейма, в котором не используются вещественные числа, а требуются минимальные арифметические возможности: сложение, вычитание и умножения на 2 для сдвига влево.

Для вывода формул алгоритма Брезенхема рассмотрим рис. 5.11а, б.

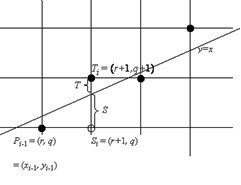а) б)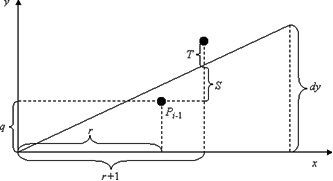

Рис. 5.11. i-й шаг алгоритма по методу Брезенхема (а). Вид отрезка после переноса в начало координат (б)