5.6 Алгоритмы удаления невидимых линий и поверхностей

Задача удаления невидимых линий и поверхностей является одной из наиболее сложных задач в компьютерной графике. Для решения данной задачи были разработаны специальные алгоритмы, целью которых является удаление тех линий ребер, поверхностей, граней или объемов, которые невидны наблюдателю. Идея алгоритмов удаления невидимых линий и поверхностей заключается в следующем: чем дальше расположен объект от точки наблюдения, тем больше вероятность, что он будет полностью или частично заслонен другим, более близким к наблюдателю, объектом. После определения расстояний или приоритетов по глубине проводится сортировка по горизонтали и по вертикали, для выяснения, будет ли рассматриваемый объект действительно заслонен объектом, расположенным ближе к точке наблюдения.

Выделяют три класса таких алгоритмов:

1. Алгоритмы, работающие в пространстве объекта. Для определения видимости данной поверхности сравнивается ее взаимное расположение с остальными поверхностями объекта в трехмерной сцене.

• Алгоритм Робертса.

2. Алгоритмы, работающие в пространстве изображения (экрана). Они основаны на нахождении точки ближайшей поверхности, которую пересекает луч зрения, проходящий через заданную точку на растре.

• Алгоритм плавающего горизонта;

• Алгоритм Коэна − Сазерленда;

• Модифицированный вариант алгоритма Коэна − Сазарленда;

• Алгоритм с использованием z-буфера;

• Метод трассировки лучей;

• Алгоритм Варнока;

• Алгоритм Вейлера − Азертона.

3. Алгоритмы, формирующие список приоритетов, работают попеременно в обеих системах координат (объекта и изображения).

• Алгоритм Ньюэла − Ньюэла − Санча (алгоритм удаления невидимых граней методом сортировки по глубине;)

Рассмотрим более подробно некоторые алгоритмы удаления невидимых линий и поверхностей.

Алгоритм Робертса

Алгоритм Робертса удаляет из каждого тела те ребра или грани, которые скрываются самим телом. Затем каждое из видимых ребер каждого тела сравнивается с каждым из оставшихся тел для определения того, какая его часть или части, если таковые есть, скрываются этими телами. При этом вычислительная трудоемкость алгоритма Робертса растет теоретически, как квадрат числа объектов. При этом математические методы, используемые в этом алгоритме, просты, мощны и точны.

Алгоритм плавающего горизонта

Алгоритм плавающего горизонта чаше всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде F(x, у, z) = 0.

Идея метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координаты z.

Алгоритм сначала упорядочивает плоскости z = const по возрастанию расстояния до них от точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, т.е. для каждого значения координаты х в пространстве изображения определяется соответствующее значение y.

Если на текущей плоскости при некотором заданном значении x соответствующее значение у на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в противном случае она невидима.

Алгоритм Коэна − Сазерленда

Алгоритм Коэна − Сазерленда предназначен для отсечения отрезков. Он был разработан Дэном Коэном и Айвеном Сазерлендом в Гарварде в 1966-1968 гг.

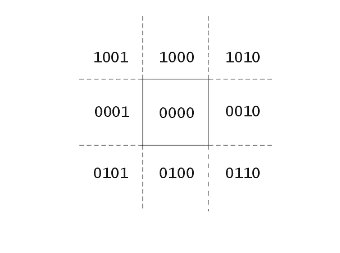
Алгоритм разделяет плоскость на девять частей прямыми, которые образуют стороны прямоугольника. Каждой из девяти частей присваивается четырехбитный код.

Окну присваивается код 0000. Конечным точкам отрезка приписывается 4-битный код "вне/внутри" в зависимости от нахождения отрезка в соответствующей подобласти. Каждому биту присваивается значение 1 в соответствии со следующим правилом.

Бит 1 − точка находится выше окна;

Бит 2 − точка находится ниже окна;

Бит 3 − точка находится справа от окна;

Бит 4 − точка находится слева от окна;

Иначе биту присваивается нулевое значение.

Алгоритм определяет код конечных точек отрезка. Если оба кода равны нулю [код₁] И [код₂] = 0000, то отрезок полностью находится в прямоугольнике. Если битовое И кодов не равно нулю, то отрезок не пересекает прямоугольник (так как это значит, что обе конечные точки отрезка находятся с одной стороны прямоугольника). В прочих случаях алгоритм выбирает конечную точку, находящуюся вне прямоугольника, находит ближайшую к ней точку пересечения отрезка с одной из линий, образующей стороны прямоугольника, и использует эту точку пересечения как новую конечную точку отрезка. Укороченный отрезок снова пропускается через алгоритм.

Рис. 5.12. Разбиение на подобласти в методе Коэна − Сазерленда