5.7 Модели расчета освещенности граней трехмерных объектов

В компьютерной графике для расчета освещенности граней объектов применяется цветовая модель RGB. Интенсивность отраженного света точек объектов вычисляют отдельно для каждой их трех составляющих цветовых компонент, а затем объединяют в результирующую тройку цветов.

При расчете освещенности граней применяют следующие типы освещения и отражения света от поверхностей.

• рассеянное;

• диффузное;

• зеркальное.

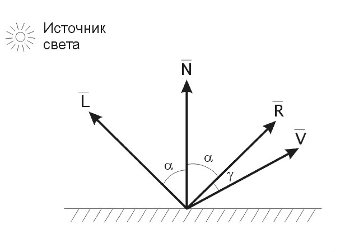
Рис. 5.13. Расчет интенсивности отраженного света

Матовые поверхности обладают свойством диффузного отражения, т. е. равномерного по всем направлениям рассеивания света. Поэтому кажется, что поверхности имеют одинаковую яркость независимо от угла обзора.

Зеркальное отражение можно получить от любой блестящей поверхности. Но блестящие поверхности отражают свет неодинаково по всем направлениям. От идеального зеркала свет отражается только в том направлении, для которого углы падения и отражения совпадают. Это означает, что наблюдатель сможет увидеть зеркально отраженный свет только в том случае, если угол 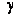(рис. 5.13) равен нулю. Для неидеальных отражающих поверхностей, таких как яблоко, интенсивность отраженного света резко падает с ростом .

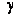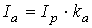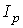Интенсивность освещения граней трехмерных объектов рассеянным светом считается постоянной в любой точке пространства. Она обусловлена множественными отражениями света от всех объектов в пространстве. При освещении трехмерного объекта рассеянным светом интенсивность отраженного света вычисляется как , где − интенсивность падающего света, 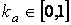− коэффициент рассеянного отражения, зависит от отражающих свойств материала грани.

Для расчета интенсивности диффузного отражения света может применяться закон косинусов Ламберта: 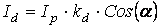, где 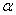− угол падения, рассчитывается как угол между направлением на источник света и нормалью к поверхности. Пусть направление на источник света представлено единичным вектором 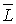, а 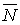− единичный вектор нормали. Тогда 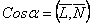− скалярное произведение векторов. Тогда 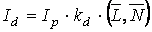, где 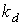− коэффициент диффузного отражения.

Метод закраски, разработанным Фонгом, основан на интерполяции векторов нормали.

Вычисление зеркально отраженного света производится также с помощью различных эмпирических моделей, которые позволяют учитывать реальную шероховатость поверхностей. Например, в модели, предложенной Фонгом, интенсивность зеркально отраженного света рассчитывается в зависимости от степени отклонения от истинного значения вектора зеркально отраженного луча света. Пусть 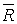− вектор зеркально отраженного луча света, а − вектор, определяющий направление на наблюдателя. Тогда интенсивность зеркально отраженного света по модели Фонга рассчитывается так: 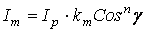, где 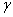− угол между векторам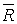и и 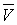. Константа n − может принимать значения от 1 до 200, в зависимости от отражающей способности материала. Большим значениям n соответствует большая степень "гладкости" или "зеркальности" поверхности. Если векторы 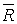и 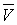− нормированы, то формула преобразуется к виду: .

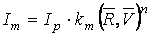Интенсивность отраженного света уменьшается обратно пропорционально квадрату расстояния от источника до наблюдателя. Поэтому можно записать формулу расчета интенсивности отраженного луча света для трех составляющих: рассеянного, диффузного и зеркального отражения с учетом расстояния:

,

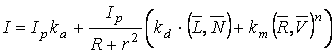где r − расстояние от точки отражения до наблюдателя, а 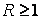− некоторая константа. Иногда, для ускорения вычислений, берут не вторую, а первую степень расстояния r.