2.2. Оцифровка звука

Оцифровка − процесс преобразования аналогового сигнала в цифровой.

Как известно, звуковая волна представляет собой сложную функцию зависимости амплитуды волны от времени. Так как же нам записать и сохранить в памяти компьютера такую функцию? Например, такие звуковые волны, как на рис. 2.3-2.4, невозможно описать с помощью аналитических функций, но при этом мы можем в каждый момент времени измерить значение амплитуды сигнала и записать в виде чисел, и таким образом запомнить эти числа. Однако значения амплитуды сигнала мы не можем записывать с бесконечной точностью, и поэтому вынуждены их округлять. Таким образом, оцифровка сигнала включает в себя два процесса − процесс дискретизации, когда мы измеряем величину сигнала на определённых дискретных промежутках, и квантования , когда эти значения ограничиваются определённым набором уровней (рис. 2.5).

Дискретизация и квантование могут выполняться в произвольном порядке. Эти процессы выполняются специальными устройствами, которые обобщенно называются аналого-цифровыми преобразователями (АЦП).

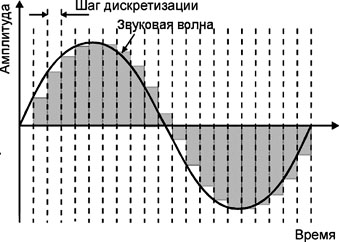
Рис. 2.5. Оцифровка

2.2.1. Дискретизация

Процесс дискретизации − это процесс получения значений величин преобразуемого сигнала в определённые промежутки времени (рис. 2.5). Как видно из рис. 2.5-2.6, в процессе оцифровки часть информации теряется. Если частота дискретизации слишком мала, тогда в процессе оцифровки некоторые детали будут утрачены. Например, при дискретизации сигнала (рис. 2.6) с недостаточной частотой мы попросту пропустим пик между точками 2 и 3, а при восстановлении аналогового сигнала по полученным дискретным значениям сигнал будет сильно отличаться от оригинала. Так как же выбрать правильную частоту дискретизации в процессе оцифровки?

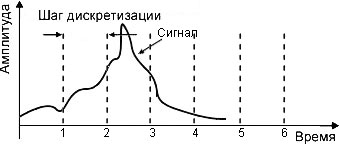
Рис. 2.6. Дискретизация с недостаточной частотой

Согласно теореме о дискретном представлении [10], если самая высокая частота из частот компонентов сигнала равна f_h, то сигнал можно будет точно восстановить в том случае, если его дискретизация была выполнена с частотой, превышающей 2f_h. Это граничное значение известно под названием частота Найквиста.

Доказательство теоремы можно очень просто проиллюстрировать. Предположим, имеется круглый диск со стрелкой, которая вращается по часовой стрелке со скоростью n оборотов в секунду. Предположим также, что это вращение оцифровывается с разной частотой дискретизации 4n, n, 4/3n, 2n раз в секунду.

Посмотрев ролики (рис. 2.7), можно увидеть, что при частоте дискретизации 4n, которая больше частоты Найквиста, диск вращается по часовой стрелке, как нам и надо. При дискретизации с частотой 4n/3 кажется, что стрелка вращается против часовой стрелки со скоростью n/3. А если выполнять дискретизацию движения нашего диска с частотой, равной 2n, то можно не определить, в какую сторону вращается стрелка, так как она будет находиться либо вверху, либо внизу.

Вывод: частота дискретизации должна превышать частоту Найквиста.

Рис. 2.7. Flash-ролик вращающейся стрелки, дискретизированной с разной частотой n (для просмотра и остановки щелкните на кнопку "пуск")