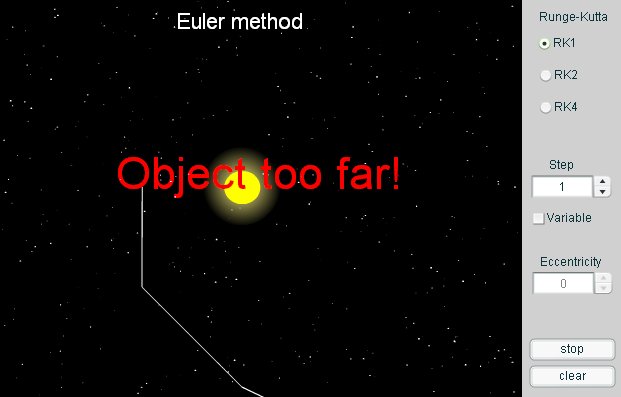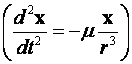
4. Анимация | 4.4. Лабораторные работы (Flash) | 4.4.12. Решение системы дифференциальных уравнений численными методами Рунге-Кутта 1, 2, 4 порядков

4.4.12. Решение системы дифференциальных уравнений численными методами Рунге-Кутта 1, 2, 4 порядков

Будем решать систему дифференциальных уравнений второго порядка для задачи двух тел

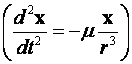
численными методами Рунге-Кутта (1,2 и 4 порядка). Рассмотрим 2 тела. Пусть это будет Солнце и какая-нибудь планета Солнечной системы.

1. Создаём новый флеш-документ, выбираем чёрный фон, размер 650x400. Так как мы рассматриваем астрономическую задачку, то нужно изобразить звездное небо. Для этого создаём новый мувик с белой небольшой точкой − это будет наша звезда. Перетаскиваем на первый слой основной сцены и называем star0. В первом кадре пишем такой код:

for (i=1;i<500;i++) {

duplicateMovieClip ("star0","star"+String(i),i);

a="star"+String(i);

setProperty (a,_x,Math.random()*550);

setProperty (a,_y,Math.random()*400);

setProperty (a,_width,Math.random()*2);

setProperty (a,_height,Math.random()*2);

}

Мы дублируем нашу звезду 500 раз и каждому дубликату присваиваем случайные координаты и случайный размер. Запустите программку, посмотрите, что получилось. Если вас всё устраивает, двигаемся дальше.

2. Создайте еще 2 мувика. В одном изобразите Солнце, вставьте его где-нибудь в центре первого слоя основной сцены и назовите sun, а во втором − планету (просто белую точку) (рис. 4.33), также вставьте на основную сцену и назовите sat (от satellite − спутник).

Рис. 4.33. Солнце и планета

3. Создаём новый слой, называем его "панель" и рисуем на нём серый прямоугольник. Я нарисовала вертикальную панель справа (рис. 4.34).

Рис. 4.34

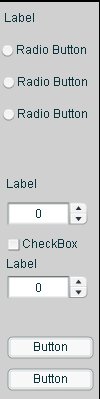
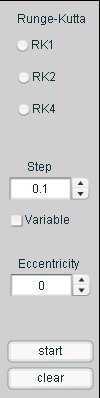
4. Создадим еще один слой − Кнопки. Открываем панель Components, выберите Label (3 раза), NumericStepper (2 раза), Radio Button (3 раза), CheckBox (1 раз) и Button (2 раза) вставляем всё это "добро" на слой кнопки, располагаем, как на картинке справа.

Продолжим. Изменим параметры компонент. Выбираем панель Properties Parameters у каждой из компонент.

Верхняя метка (Label). В параметрах изменим Text на Runge-Kutta, остальные параметры оставим без изменения.

Следующие 3 − Radio Button. В Instance name напишем rb1, rb2, rb4, соответственно. В параметрах изменим Label на RK1, RK2, RK4. В selected для RK1, RK2 выберите False, а в Selected для RK4 выберите True. Когда запустите программу (Ctrl+Enter), у вас будет выделен метод 4-го порядка.

Вторая метка. В параметрах изменим Text на Step.

1 Numeric Stepper. В Instance name напишем shag. В параметрах:

maximum 1;

minimum 0.01;

step Size 0.01;

value 0.1.

CheckBox. В Instance name напишем varstep. В параметрах изменим Text на Variable.

Третья метка. В параметрах изменим Text на Eccentricity.

2 Numeric Stepper. В Instance name напишем ecc. В параметрах:

maximum 0.9;

minimum −1;

step Size 0.1;

value 0.0.

Button. В Instance name напишем pl. В параметрах изменим Label на Start.

Button. В Instance name напишем cl. В параметрах изменим Label на Clear.

Должно получиться как на рисунке справа.

Наверно, вы уже поняли, что RK1, RK2, RK4 отвечают за порядок численного метода Рунге-Кутта (1, 2 или 4 порядок), Step − за постоянный шаг интегрирования, Variable − за переменный шаг интегрирования, Eccentricity − за эксцентриситет орбиты нашей планеты, кнопка Start − за запуск программы, а Clear − за очистку экрана.

5. Создайте новый слой, назовите его Action. Вставьте динамический текст в центр, назовите его mess (от message), установите в свойствах текста: 45-й размер шрифта и красный цвет. Вставьте еще один динамический текст по центру и вверху фона, назовите его method, установите в свойствах текста: 20-й размер шрифта и белый цвет.

6. В первый кадр слоя Action (Actions Frame) вставьте такой код:

// Создаём массивы

f=Array(4); x=Array(4); f1=Array(4); x1=Array(4);

f2=Array(4); f3=Array(4);

// Задаём начальные значения эксцентриситета ex, гравитационный параметр mu, начальные значения для координат x[5], x[2] и скоростей x[3], x[4].

ex=ecc.value;

mu=1;

x[5]=−1; x[2]=0; x[3]=0; x[4]=Math.sqrt(1+ex);

// Проверяем, стоит ли галочка на переменном шаге varstep, если да, то вычисляем начальный шаг интегрирования

if (varstep.selected){

hh=(x[3]*x[3]+x[4]*x[4])/2−1/Math.sqrt(x[5]*x[5]+x[2]*x[2]);

aa=−0.5/hh;

dt=shag.value*Math.sqrt(x[5]*x[5]+x[2]*x[2])/aa;

} else { dt=shag.value;};

// Задаём начальное положение планеты относительно Солнца

kx=100; ky=100;

sat._x=sun._x−100;

sat._y=sun._y;

// Создаём функции для использования в итерационных схемах методов

function func1(a,b){

return −mu*a/(b*b*b);

};

function func2(a,b){

return a+dt*b;

};

function func3(a,b){

return 0.5*dt*(a+b);

};

cl=true;

// Для кнопки play/stop

cond=0;

// Останавливаемся в первом кадре, пока не нажмём на кнопку start

stop();

7. Нажмите F6, появится 2-й кадр, в него вставьте следующий код:

// Меняем момент времени, эксцентриситет

t=t+dt;

ex=ecc.value;

// Метод Рунге-Кутта 1-го порядка (RK1), или как его еще называют метод Хойна

if (rb2.selected){

method.text='Heun method';

r=Math.sqrt(x[5]*x[5]+x[2]*x[2]);

f[5]=x[3]; f[2]=x[4]; f[3]=func1(x[5],r); f[4]=func1(x[2],r);

for (i=1;i<5;i++){

x1[i]=func2(x[i],f[i]);

}

r1=Math.sqrt(x1[5]*x1[5]+x1[2]*x1[2]);

f1[5]=x1[3]; f1[2]=x1[4]; f1[3]=func1(x1[5],r1); f1[4]=func1(x1[2],r1);

for (i=1;i<5;i++){

x[i]=x[i]+func3(f[i],f1[i]);

};

}

// Метод Эйлера (RK2)

if (rb1.selected){

method.text='Euler method';

r=Math.sqrt(x[5]*x[5]+x[2]*x[2]);

f[5]=x[3]; f[2]=x[4]; f[3]=func1(x[5],r); f[4]=func1(x[2],r);

for (i=1;i<5;i++){

x[i]=x[i]+2*func3(f[i],0);

};

// Метод Рунге-Кутта 4-го порядка (классический метод)

if (rb4.selected){

method.text='Classical method';

r=Math.sqrt(x[5]*x[5]+x[2]*x[2]);

f[5]=x[3]; f[2]=x[4]; f[3]=func1(x[5],r); f[4]=func1(x[2],r);

for (i=1;i<5;i++){

x1[i]=x[i]+dt*0.5*f[i];

};

r1=Math.sqrt(x1[5]*x1[5]+x1[2]*x1[2]);

f1[5]=x1[3]; f1[2]=x1[4]; f1[3]=func1(x1[5],r1); f1[4]=func1(x1[2],r1);

for (i=1;i<5;i++){

x1[i]=x[i]+dt*0.5*f1[i];

};

r1=Math.sqrt(x1[5]*x1[5]+x1[2]*x1[2]);

f2[5]=x1[3]; f2[2]=x1[4]; f2[3]=func1(x1[5],r1); f2[4]=func1(x1[2],r1);

for (i=1;i<5;i++){

x1[i]=x[i]+dt*f2[i];

};

r1=Math.sqrt(x1[5]*x1[5]+x1[2]*x1[2]);

f3[5]=x1[3]; f3[2]=x1[4]; f3[3]=func1(x1[5],r1); f3[4]=func1(x1[2],r1);

for (i=1;i<5;i++){

x[i]=x[i]+dt/6*(f[i]+2*(f1[i]+f2[i])+f3[i]);

};

// Проверяем, как далеко находится планета, если далеко, то пишем сообщение и останавливаемся

if (Math.abs(x[5])>100 or Math.abs(x[2])>100){

mess.text='Object too far!';

stop();

};

// Если выбран переменный шаг, то пересчитываем его

if (varstep.selected){

hh=(x[3]*x[3]+x[4]*x[4])/2−1/Math.sqrt(x[5]*x[5]+x[2]*x[2]);

aa=−0.5/hh;

dt=shag.value*Math.sqrt(x[5]*x[5]+x[2]*x[2])/aa;

} else { dt=shag.value;};

8. Нажмите еще раз F6. В 3-й кадр вставьте такой код:

// Определяем стиль кривой (толщину, цвет)

lineStyle(1, 0xFFFFFF)

// Запоминаем старые координаты планеты

xold=sat._x; yold=sat._y;

// Вычисляем новые координаты планеты, переводя их в пикселы (*kx)

sat._x=Math.round(x[5]*kx+sun._x);

sat._y=Math.round(x[2]*ky+sun._y);

// Рисуем кривую от старых координат к новым

beginFill(0xFFFFFF);

moveTo(sat._x,sat._y);

curveTo(sat._x,sat._y,xold,yold);

endFill();

// Возвращаемся во 2-й кадр

gotoAndPlay(2);

9. Создайте еще один слой, назовите его "код для кнопок" и напишите:

// Кнопка play/stop

pl.onRelease=function(){

if (cond!=1) {

ex=ecc.value;

if (varstep.selected){

hh=(x[3]*x[3]+x[4]*x[4])/2−1/Math.sqrt(x[5]*x[5]+x[2]*x[2]);

aa=−0.5/hh;

dt=shag.value*Math.sqrt(x[5]*x[5]+x[2]*x[2])/aa;

} else { dt=shag.value;};

ecc.enabled=false;

if (cl==true){

x[5]=−1; x[2]=0; x[3]=0; x[4]=Math.sqrt(1+ex);

};

cl=false;

play();

pl.label='stop';

cond = 1;

} else {

if (varstep.selected){

hh=(x[3]*x[3]+x[4]*x[4])/2−1/Math.sqrt(x[5]*x[5]+x[2]*x[2]);

aa=−0.5/hh;

dt=shag.value*Math.sqrt(x[5]*x[5]+x[2]*x[2])/aa;

} else { dt=shag.value;};

ex=ecc.value;

stop();

cond = 0;

pl.label='start';

};

// Кнопка clear

cl.onRelease=function(){

clear();

ex=ecc.value;

sat._x=sun._x−100; sat._y=sun._y;

xold=sat._x; yold=sat._y;

x[5]=−1; x[2]=0; x[3]=0; x[4]=Math.sqrt(1+ex);

if (varstep.selected){

hh=(x[3]*x[3]+x[4]*x[4])/2−1/Math.sqrt(x[5]*x[5]+x[2]*x[2]);

aa=−0.5/hh;

dt=shag.value*Math.sqrt(x[5]*x[5]+x[2]*x[2])/aa;

} else { dt=shag.value;};

cl=true;

ecc.enabled=true;

Kepler.enabled=true;

mess.text='';

mess._x=−305; mess._y=34;

per=0;

//Для кнопки play

cond = 0;

pl.label='start';

stop();

};

10. Программа готова! Запустите её Ctrl+Enter. При нажатии на кнопку start кнопка start превратится в кнопку stop, планета начнёт двигаться вокруг Солнца, очерчивая свою орбиту с эксцентриситетом, который вы выберете. Во время рисования вы можете менять метод (RK1, RK2, RK4), размер шага (step), использовать переменный шаг интегрирования (variable), но при этом кнопка с эксцентриситетом заблокируется, и вы сможете выбрать другой эксцентриситет только после очистки экрана (кнопка clear). Если ваша планета улетит довольно далеко, то программка остановит счёт и выдаст вам сообщение, что объект слишком далеко "Object too far!".