1.5. Системы высот

1.5.1. Определение системы высот

Для передачи высот от начала нивелирной сети - точки А на поверхности геоида (рис. 1.8) к точке В, методом геометрического нивелирования суммируют все превышения, измеренные на всех станциях

Нивелирные сети

Нивелирные сети - это сети построенные методом геометрического нивелирования.

Геометрическое нивелирование

Геометрическим нивелированием называют процесс измерения разностей высот точек местности (превышений) с помощью горизонтального луча визирования геодезического прибора.

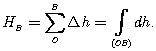(1.44)

Получаемая подобным образом высота зависит от пути нивелирования. Это вызвано непараллельностью уровенных поверхностей, обусловленной наличием аномальных масс.

Уровенная поверхность

Уровенная поверхность в геодезии, поверхность, во всех точках которой потенциал силы тяжести имеет одинаковую величину. Направление нормали к У.п. совпадает с направлением силы тяжести, т.е. с линией отвеса. Примером У.п. является поверхность жидкости, находящейся в равновесии. У.п. гравитационного поля Земли, совпадающая со средним уровнем воды в океанах, называется геоидом и принимается за математическую поверхность Земли, или "уровень моря", от которого отсчитывают высоты точек земной поверхности. Форма У.п. весьма сложна и зависит от внутреннего строения Земли.

Проведем в точках А и М уровенные (эквипотенциальные) поверхности W_А=const и W_M=const. Уровенная поверхность, проходящая через точку А и совпадающая с уровнем моря, является геоидом. Следует иметь в виду, что топографическая поверхность моря в спокойном состоянии не является эквипотенциальной поверхностью. Несовпадение между ними может достигать 2.5 м. Проведем также силовые линии АА₀ и ММ₀ до их пересечения с эллипсоидом. Ортометрической высотой называется расстояние между геоидом и данной точкой, отсчитываемое по силовой линии, проходящей через точку. Ортометрическая высота для точки М может быть получена по формуле

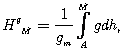(1.45)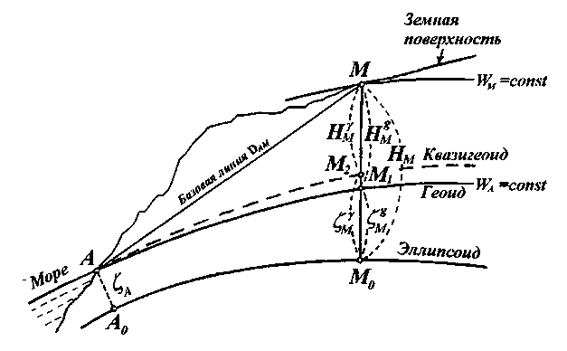

где g_m - среднее значение реальной силы тяжести на отрезке MM₁, a g - измеренное значение силы тяжести вдоль линии нивелирования AM. Без ущерба для точности ортометрическую высоту можно отсчитывать по нормали к эллипсоиду. Недостатком ортометрических высот является то, что для их точного вычисления требуется знание строения земной коры, иными словами, точность вычисления ортометрических высот зависит от принятой гипотезы о строении земной коры.

Рис. 1.8. Поверхности относимости в системах высот

От этого недостатка свободна предложенная М.С. Молоденским система нормальных высот, в которых высота точки может быть вычислена по формуле

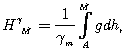(1.46)

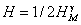где g_m - значение нормальной силы тяжести на высоте

над эллипсоидом. На поверхности эллипсоида нормальная сила тяжести вычисляется по формуле Гельмерта (или формуле Сомильяна (1.34)

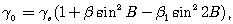(1.47)

где

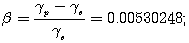(1.48)

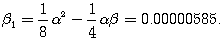(1.49)

Нормальная сила тяжести во внешнем пространстве находится по формуле

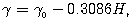(1.50)

где Н - высота над эллипсоидом. Значения коэффициентов приводятся для эллипсоида со сжатием a =1/298.257+0.001 и силе тяжести на экваторе g_e =978033 мГал.