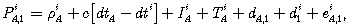Полученные выше модели уравнений псевдодальности (6.17) и фазы несущей (6.35) не являются линейными. Покажем в качестве примера линеаризацию уравнения для псевдодальности для L1. Линеаризация других уравнений происходит аналогичным путем. Уравнение наблюдений для псевдодальности возьмем в виде

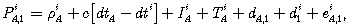(6.36)

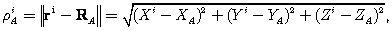(6.37)

Для линеаризации нужны приближенные (априорные) величины для векторов положений спутника и приемника в общеземной системе. При этом, чтобы ограничиваться первыми членами разложений, необходимы их значения, достаточно близкие к истинным значениям. Обозначим их как

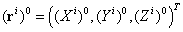- приближенное положение спутника на орбите;

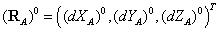- приближенное положение пункта. Поправки к приближенным положениям спутника и приемника обозначим соответственно как 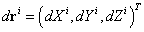и 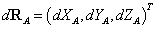. Таким образом,

(6.38)

(6.39)

Подстановка выражений (6.38) и (6.39) в (6.37) с последующим разложением в ряд Тейлора при ограничении членами первого порядка дает

(6.40)

Первый член в правой части выражения (6.40) является приближенным значением геометрической дальности

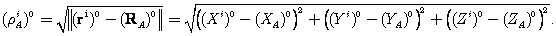(6.41)

Величина uⁱ_A является вектором частных производных от геометрической дальности по координатам:

(6.42)

Она вычисляется по приближенным значениям координат и представляет собой единичный вектор топоцентрического направления на спутник.

Отметим, что поправку к вектору положения спутника dr^l можно выразить через поправки в элементы орбиты и использовать измерения псевдодальности (или фазы) для уточнения параметров движения или возмущающих сил, как это делается в орбитальном и динамическом методах космической геодезии.

Другая проблема, связанная с уравнениями (6.17) и (6.35), состоит в том, что находящиеся в них параметры поправок часов, тропосферной и ионосферной задержек, фазовая неоднозначность (только в уравнении (7.35)) и другие параметры являются линейно зависимыми и для них требуется другое представление.