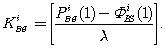Вариант локального дифференциального метода с использованием фазовых измерений обычно применяется в режиме кинематики и называется кинематикой реального времени или RTK (Антоновича, 2006)

Первый шаг при вычислении поправки для фазы несущей заключается в определении из наблюдений первой эпохи на базовой станции целого числа K_BSⁱ:

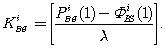(8.6)

В уравнении (8.6) для измеренной псевдодальности P_BSⁱ(1) и фазы F_BSⁱ несущей, выраженной в единицах расстояния, используются обычные символы. Квадратные скобки здесь означают оператор округления до ближайшего целого числа. Поскольку неоднозначность N_BSⁱ(1) невозможно определить в процессе измерения фазы, ее величина устанавливается произвольно регистром счетчика. Это и есть показание F_BSⁱ(1). Определим дальность по фазе несущей W_BSⁱ(1) как

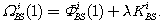(8.7)

Численное значение W_BSⁱ(1) близко к кодовой псевдодальность P_BSⁱ(1) из-за способа, которым определено целое число K_BSⁱ по формуле (8.6). Для каждого спутника, наблюдавшегося на базовой станции BS, можно вычислить дальность W_BSⁱ(1) по фазе несущей и топоцентрическое расстояние r_Aⁱ(1). Последнее выводится по принятым (эталонным) координатам опорного приемника и эфемеридному положению спутника по формулам (7.3), (7.4). Невязка для дальности по фазе несущей равна

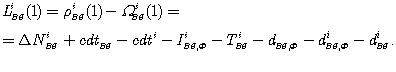(8.8)

Член DN_BSⁱ присутствует потому, что в (8.6) используется округление. Насколько мало DN_BSⁱ, настолько будет мала невязка L_BSⁱ(1). Средняя невязка для всех наблюденных спутников на опорном пункте для эпохи 1 равна

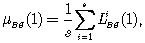(8.9)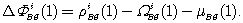

(8.10)

Изменение невязки от одной эпохи к следующей получается как

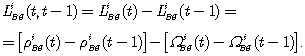(8.11)

Средняя невязка в эпоху i вычисляется по формуле

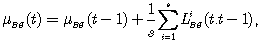(8.12)

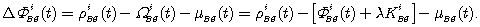(8.13)

Вторая часть этого уравнения получается после подстановки (8.8) в формулу для фазовой дальности. Фазовая поправка (8.13) эпохи t передается на мобильную станцию MS, где измеренная фаза несущей исправляется:

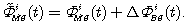(8.14)