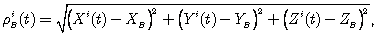 (9.10 a)
(9.10 a)9.3. Кинематическое относительное позиционирование
В кинематическом позиционировании приемник на известной точке А в начале базовой линии остается фиксированным. Второй приемник перемещается, а его положения должны определяться в произвольные эпохи. Движение мобильного приемника отражается в неявной форме в уравнениях для одинарных, двойных и тройных разностей через геометрическую дальность. Возьмем мобильную станцию В и спутник i, геометрическое расстояние в статическом режиме дается как
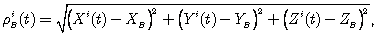 (9.10 a)
(9.10 a)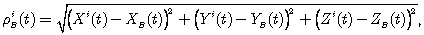 (9.10 б)
(9.10 б)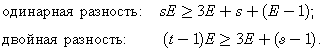 (9.11)
(9.11)Например, соотношение
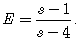 (9.12)
(9.12)Непрерывное движение подвижного приемника ограничивает доступные данные для определения его положения в одну эпоху. Но ни одна из приведенных выше моделей не обеспечивает приемлемое решение при Е=1. Поэтому эти модели модифицируются: число неизвестных уменьшается посредством удаления неизвестных неоднозначностей, то есть неоднозначности предполагаются известными. Для одинарных разностей это имеет двойной эффект: во-первых, s неоднозначностей можно удалить, и, во-вторых исчезает дефект ранга из-за известных неоднозначностей, так что необходимо определять только Е неизвестных поправок часов. Поэтому требование к модифицированным наблюдениям для одинарных разностей состоит в том, чтобы sE>=4E и для одной эпохи уменьшается до s>=4. Подобным образом для двойных разностей s-1 неоднозначностей удаляются в (9.12) так, что в результате (s-1).E>=3.E, что для одной эпохи уменьшается до s>=4.
Следовательно, модели для одинарных и двойных разностей заканчиваются фундаментальным требованием одновременного наблюдения не менее четырех спутников.