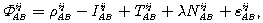 (9.26)
(9.26)9.7. Функциональные модели в относительном позиционировании
Двойная разность фаз. В разделе 6 были показаны линейные модели и для кодовых дальностей, и для фазы несущей. В случае относительного позиционирования ограничим исследование фазами несущей, поскольку должно быть ясно, как перейти от расширенной фазовой модели к модели по кодам. Более того, линеаризация и установление системы линейных уравнений остаются в принципе одинаковыми для фазы и фазовых комбинаций и могут выполняться аналогично для каждой модели. Поэтому для детального исследования здесь выбраны двойные разности фаз. Модель двойной разности фаз FABij, полученной по наблюдениям с пунктов А и В на спутники i и j и представленной в единицах расстояния, имеет вид
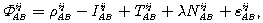 (9.26)
(9.26)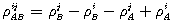 (9.27)
(9.27)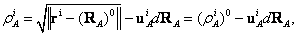 (9.28)
(9.28)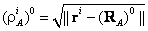 - значение геометрической дальности, вычисленной по координатам
спутника, исправленным за вращение Земли (см. формулу (7.4)) и
априорным координатам пункта (RA)0. Теперь двойную разность геометрических
дальностей можно представить в виде
- значение геометрической дальности, вычисленной по координатам
спутника, исправленным за вращение Земли (см. формулу (7.4)) и
априорным координатам пункта (RA)0. Теперь двойную разность геометрических
дальностей можно представить в виде
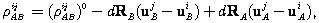 (9.29)
(9.29)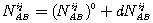 (9.30)
(9.30)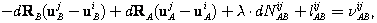 (9.31)
(9.31)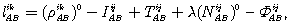 (9.32)
(9.32)Заметим, что координаты одной точки, например, А, для относительного позиционирования должны быть известны. Более важно, что известная точка А уменьшает число неизвестных на три, поскольку
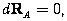 (9.33)
(9.33)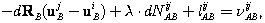 (9.34)
(9.34) (9.35)
(9.35)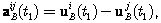 (9.36)
(9.36)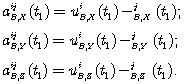 (9.37)
(9.37)Заметим, что для одной эпохи система имеет больше неизвестных, чем уравнений наблюдений, для двух эпох и четырех спутников число уравнений и неизвестных равны между собой, поэтому v=0, но при большем числе измерений получается преопределенная система:
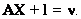 (9.38)
(9.38)Подобным образом можно получить уравнение поправок для тройных разностей фаз и других видов разностей и комбинаций фазы.