2. Метод разложения в ряд Тейлора

Одним из старейших методов решения дифференциальных уравнений является метод разложения в ряд Тейлора.

Обратимся к скалярному случаю. Пусть требуется найти решение уравнения (1.1)

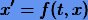
для заданного значения 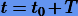при начальном условии 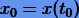. Потребуем, чтобы ƒ была аналитична в точке 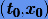. Дифференцируя уравнение по t, будем иметь

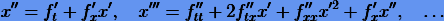
Подставляя , последовательно получаем

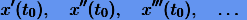(2.1)

Таким образом, при достаточно малом T приближенное решение в окрестности t₀ можно представить в виде ряда Тейлора

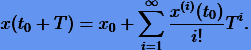(2.2)

Оборвем (усечем) ряд (2.2) на p-м члене. Тогда получим приближенную формулу р-порядка

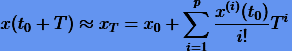(2.3)

с погрешностью

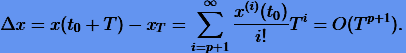(2.4)

Нетрудно видеть, что при малых T погрешность Δx (ошибка усечения) будет определяться главным образом первым членом ряда (2.4):

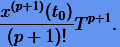(2.5)

Его называют главным членом погрешности.

Если для 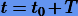ряд Тейлора (2.2) расходится или ошибка приближенной формулы (2.3) довольно большая, то прибегают к так называемому пошаговому интегрированию. Разбивают 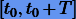на малые отрезки 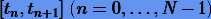, где 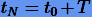, и последовательно получают приближенные решения по формуле

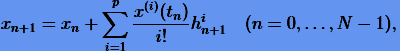(2.6)

где 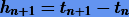— n-й шаг интегрирования.

Рассмотрим частные случаи. Для p = 1 и p = 2 с постоянным шагом h имеем формулы

(2.7)

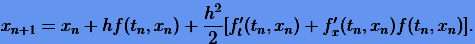(2.8)

Главным недостатком метода разложения в ряд Тейлора является то, что для получения производных (2.1) необходимо знать производные от ƒ как функции t и x. Очевидно, если ƒ — сложная функция, получение этих производных может представлять собой весьма утомительное занятие. В связи с этим методы разложения в ряд Тейлора редко используются на практике.

Впрочем, в небесной механике имеет место ряд важных с прикладной точки зрения задач, где, используя специфику дифференциальных уравнений, удается получить достаточно простые рекуррентные соотношения для временных производных в разложениях Тейлора. В 1957 г. К. Стеффенсен путем введения новых вспомогательных переменных вывел подобные соотношения для численного интегрирования уравнений планетной задачи.

Рассмотрим идею метода Стеффенсена на примере нормализованных уравнений задачи двух тел:

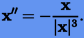(2.9)

Если ввести вспомогательные переменные 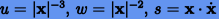и , то уравнение (2.9) можно привести к дифференциально-алгебраической системе уравнений с квадратичными правыми частями

(2.10)

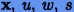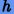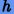Тогда, подставляя в (2.10) степенные ряды для и по малому параметру и приравнивая коэффициенты при одинаковых степенях , получим для них рекуррентные формулы:

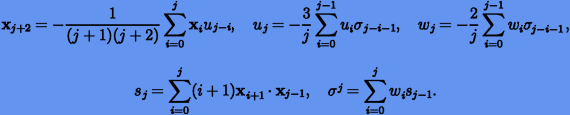(2.11)

При этом 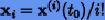Коэффициенты нулевого порядка 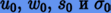вычисляются по начальным данным .

Подобный подход также применяется и для численного интегрирования более сложных дифференциальных уравнений небесной механики, в частности, задачи нескольких тел в классической постановке.