3. Методы Рунге − Кутты

В начале прошлого века К.Д.Т. Рунге, а затем К. Хойн и М.В. Кутта предложили подход, основанный на построении приближенной формулы близкой к (2.3), не содержащей производных от ƒ.

3.1. Первый метод Рунге

Пусть мы имеем задачу Коши

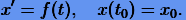(3.1)

Для ее решения применим метод Эйлера (2.7). На первом шаге решение будет

(3.2)

Мы знаем, что метод Эйлера имеет ошибку 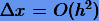. Однако порядок ошибки можно повысить, если в (3.2) функцию ƒ вычислять не в 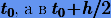(правило средней точки), т.е. если вместо (3.2) использовать схему интегрирования

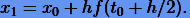(3.3)

Действительно, разложим 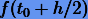в степенной ряд Тейлора

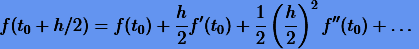
и подставим в (3.3). Поскольку , будем иметь

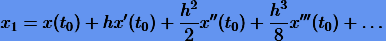(3.4)

Мы видим, что (3.4) совпадает с разложением точного решения 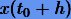до третьего члена. Следовательно, ошибка формулы (3.3) будет порядка h³.

Рунге (1895) поставил вопрос: нельзя ли распространить метод (3.3) на уравнение 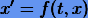? По аналогии с (3.3) первый шаг должен иметь вид

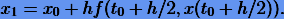
Но какое значение взять для ? За неимением лучшего Рунге предлагает использовать один шаг метода Эйлера длины h/2. Тогда получаем

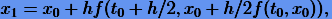(3.5)

или

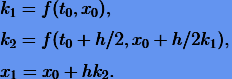(3.6)

Чтобы определить порядок решения (3.5), разложим его в ряд

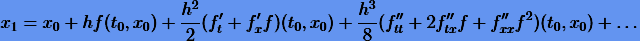(3.7)

и сравним с разложением точного решения :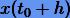

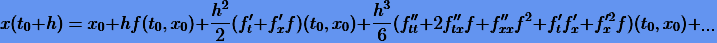(3.8)

Вычитая (3.7) из (3.8), получаем погрешность

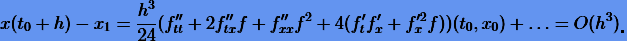(3.9)

Таким образом, мы получили усовершенствованный метод Эйлера второго порядка, где не требуется находить производные от f, какие необходимы в методе разложения в ряд Тейлора (2.8).