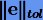 — заданная точность. Потребуем, чтобы на следующем шаге выполнялось равенство
— заданная точность. Потребуем, чтобы на следующем шаге выполнялось равенство3.11.4. Выбор шага
В интеграторе Эверхарта контроль шага интегрирования осуществляется по величине последнего члена в (3.58). Пусть 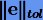 — заданная точность. Потребуем, чтобы на следующем шаге выполнялось равенство
— заданная точность. Потребуем, чтобы на следующем шаге выполнялось равенство
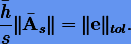
Отсюда, используя последнее соотношение в (3.56), получаем оценку
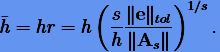 |
(3.60) |
Очевидно, при разбиениях Гаусса недостаток такой оценки состоит в том, что шаг по ней выбирается как для решения порядка s − 1, поэтому, вообще говоря, она не обеспечивает сохранение требуемой локальной точности.
Во избежание слишком больших (и малых) локальных ошибок на r следует наложить ограничение:
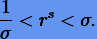 |
(3.61) |
Для того чтобы величина последнего члена в (3.58) была ограничена в пределах одного порядка, значение  должно быть равно
должно быть равно 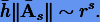 . Это следует из того факта, что
. Это следует из того факта, что
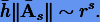
Выполнение обоих неравенств проверяется лишь в начале интегрирования при выборе стартового шага: если (3.60) не выполняется, то интегрирование повторяется с новым шагом 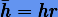 и так далее, пока не выполнится условие (3.60). Обычно для получения стартового шага требуется не более 4 итераций. В дальнейшем для ограничения r проверяется только правое неравенство: если неравенство не выполняется, то r принимает значение правого предела.
и так далее, пока не выполнится условие (3.60). Обычно для получения стартового шага требуется не более 4 итераций. В дальнейшем для ограничения r проверяется только правое неравенство: если неравенство не выполняется, то r принимает значение правого предела.
Начальное приближение стартового шага получается из оценки, подобной (3.59) для s = 2:
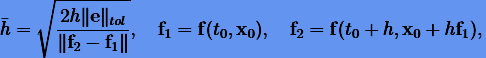 |
(3.62) |
где h — малая величина. Если h настолько мала, что в компьютерной арифметике  , она увеличивается в 10 раз и оценка повторяется снова.
, она увеличивается в 10 раз и оценка повторяется снова.