3.11.2. Интегрирование на шаге

Величины α определяются по f, которые, в свою очередь, вычисляются по решениям x. Согласно (3.46) эти решения будем задавать как

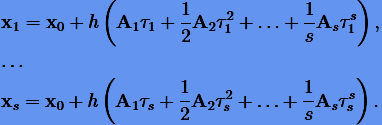(3.54)

Формулы (3.53) представляют собой неявные уравнения относительно x, поэтому они решаются итерационным способом.

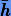Для получения начального приближения на следующем шаге используется информация о коэффициентах A на текущем шаге h. Безразмерная независимая переменная следующего шага будет 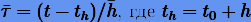. Отсюда

(3.55)

где 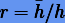. Согласно (3.45)

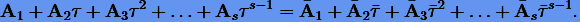(3.56)

Подставляя (3.54) в (3.55) и приравнивая коэффициенты при одинаковых степенях , получаем

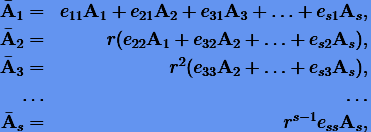(3.57)

где — числа арифметического треугольника, вычисляемые по рекуррентным формулам

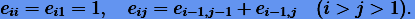(3.58)

Пользуясь соотношениями (3.51) для 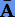, будем иметь начальное приближение .

Оценку 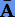для 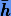можно существенно улучшить, если к ней добавлять поправку ΔA, получаемую как разность между значениями A после итераций и оценкой 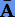на текущем шаге h.

Каждая итерация выполняется следующим образом. Сначала определяется решение x₁, из которого по первой формуле (3.49) находится значение α₁. Далее определяется x₂, по которому улучшается α₂, и так до x_s. Как правило, для получения достаточно хороших α необходимо всего лишь 2 итерации, очень редко — 3.

Как только величины α получены, решение на шаге 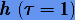будет

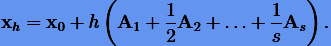(3.59)

В начале интегрирования, на первом шаге, в качестве выбирают нулевые значения и запускается вышеописанный итерационный процесс. Если начальный шаг достаточно большой, чтобы обеспечить заданную локальную точность, то его следует уменьшить. При оптимально выбранном шаге высокая точность α достигается уже на 4-й итерации.