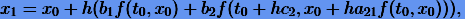
3.2. Методы Рунге − Кутты второго порядка
Методы Рунге − Кутты второго порядка имеют общий вид
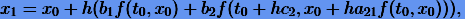 |
(3.10) |
или
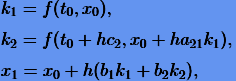 |
(3.11) |
где 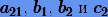 — постоянные, подлежащие определению. Нетрудно видеть, что схема Рунге (3.6) есть частный случай (3.11).
— постоянные, подлежащие определению. Нетрудно видеть, что схема Рунге (3.6) есть частный случай (3.11).
Определим постоянные схемы интегрирования так, чтобы она имела второй порядок. Разложим (3.10) в ряд
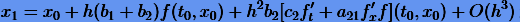
и сравним с разложением точного решения
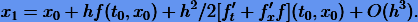
Следовательно, чтобы схема интегрирования имела второй порядок, постоянные должны удовлетворять уравнениям
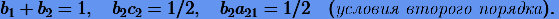 |
(3.12) |
Система уравнений (3.12) дает однопараметрическое семейство решений, которое можно представить в виде
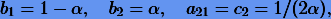
где 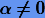 — свободный параметр.
— свободный параметр.
Например, при α = 1/2 имеем формулу Хойна
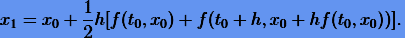 |
(3.13) |
Это явная формула, в которой требуются два вычисления функции f на шаге.