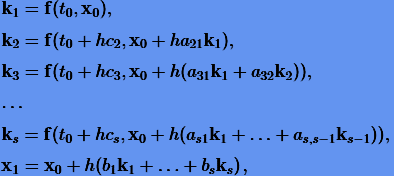
3.3. Явные методы Рунге − Кутты

Рунге продемонстрировал идею получения новых методов только для низких порядков. Но именно Кутта (1901) сформулировал общую схему того, что теперь называется методами Рунге − Кутты. Дадим определение этих методов применительно к системе (1.8).

Метод

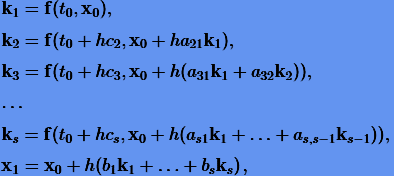(3.14)

или

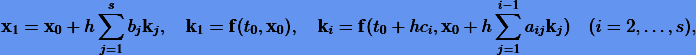
называется s-этапным (s-стадийным) явным методом Рунге − Кутты для задачи (1.8). Обычно коэффициенты c_i удовлетворяют условиям

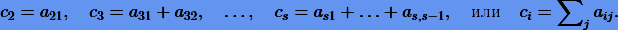
Кроме того, поскольку согласно (3.14)

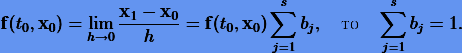
Метод Рунге − Кутты (3.14) имеет порядок р, если для (1.8)

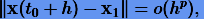(3.15)

т.е. если ряды Тейлора для точного решения 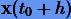и для x₁ совпадают до члена 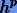включительно.

Символически методы Рунге − Кутты (3.14) принято представлять в виде таблицы

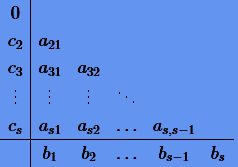(3.16)

В качестве примера рассмотрим явный 4-этапный классический метод Рунге − Кутты четвертого порядка для произвольного шага n + 1:

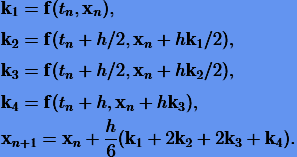(3.17)

Классический метод имеет табличный вид

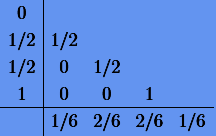(3.18)