3.4. Условия порядка
Коэффициенты 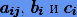 определяются из так называемых условий порядка. Эти условия получаются из разложения приближенного решения в ряд Тейлора и сравнения его с разложением точного решения. При этом коэффициенты определяются таким образом, чтобы получить в разложениях как можно больше попарно одинаковых первых членов.
определяются из так называемых условий порядка. Эти условия получаются из разложения приближенного решения в ряд Тейлора и сравнения его с разложением точного решения. При этом коэффициенты определяются таким образом, чтобы получить в разложениях как можно больше попарно одинаковых первых членов.
Подобные манипуляции мы выполняли для определения коэффициентов в методах Рунге − Кутты второго порядка. В конечном итоге получили условия второго порядка (3.12). Таким же образом нетрудно вывести условия третьего порядка. Они будут
Условия для более высоких порядков чрезвычайно громоздки, и поэтому мы не будем их расматривать.
Очевидно, именно условия порядка задают связь между порядком метода p и числом этапов (числом обращения к функции правых частей) s. К сожалению, только до четвертого порядка p = s. Для методов более высокого порядка  .
.
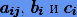 определяются из так называемых условий порядка. Эти условия получаются из разложения приближенного решения в ряд Тейлора и сравнения его с разложением точного решения. При этом коэффициенты определяются таким образом, чтобы получить в разложениях как можно больше попарно одинаковых первых членов.
определяются из так называемых условий порядка. Эти условия получаются из разложения приближенного решения в ряд Тейлора и сравнения его с разложением точного решения. При этом коэффициенты определяются таким образом, чтобы получить в разложениях как можно больше попарно одинаковых первых членов.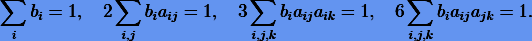
 .
.