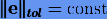 — допустимая величина локальной погрешности. Нам необходимо подобрать такой шаг интегрирования
— допустимая величина локальной погрешности. Нам необходимо подобрать такой шаг интегрирования 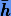 , который бы обеспечивал заданную величину локальной погрешности для метода Рунге − Кутты порядка р.
, который бы обеспечивал заданную величину локальной погрешности для метода Рунге − Кутты порядка р.3.5.3. Выбор шага
Как мы уже знаем, возможность использования переменного шага необходима для обеспечения допустимой величины локальной погрешности, что весьма важно при сложном поведении функции f. Мы предлагаем следующий алгоритм выбора шага.
Пусть 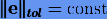 — допустимая величина локальной погрешности. Нам необходимо подобрать такой шаг интегрирования
— допустимая величина локальной погрешности. Нам необходимо подобрать такой шаг интегрирования 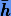 , который бы обеспечивал заданную величину локальной погрешности для метода Рунге − Кутты порядка р.
, который бы обеспечивал заданную величину локальной погрешности для метода Рунге − Кутты порядка р.
Итак, выполняем интегрирование на шаге h, и на двух шагах h/2. В результате получаем два решения 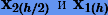 , по которым затем вычисляем величину локальной погрешности на шаге h, используя главный член погрешности (3.26):
, по которым затем вычисляем величину локальной погрешности на шаге h, используя главный член погрешности (3.26):
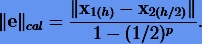
Тогда новый шаг 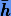 определяем по формуле
определяем по формуле
 |
(3.29) |
которая фактически получается из оценок

Далее обычно применяют экстраполяцию (3.27), с тем чтобы дополнительно повысить точность численного решения.
Следует заметить, если поведение решения довольно гладкое, то оценку (3.29) можно применять не для текущего, а для следующего шага, т.е. использовать формулу
 |
(3.30) |