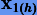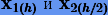3.5.2. Практическая оценка погрешности. Экстраполяция численного решения

Для практики оценка погрешности необходима с целью выбора оптимального шага: с одной стороны достаточно малого для обеспечения требуемой точности, но с другой — достаточно большого во избежание бесполезной вычислительной работы.

Очевидно, полученные нами оценки погрешностей (3.19) и (3.21) не представляют практической ценности, поскольку являются качественными.

Самый старый способ, который еще использовал Рунге для практической оценки точности численного решения, состоит в повторении вычислений с уменьшенной вдвое длиной шага и сравнении результатов. Рассмотрим этот способ подробнее.

Предположим, мы используем некоторый метод Рунге − Кутты порядка p. Отправляясь от начальных значений x₀, получим сначала численное решение 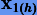на шаге h. Затем повторим интегрирование от x₀, последовательно выполнив два шага длиной h/2. При этом получим соответственно два численных решения .

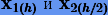Разложим погрешность 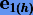на шаге h в степенной ряд. Поскольку наш метод имеет порядок p, то разложение представимо в виде

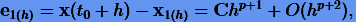(3.22)

где C выражается через производные (p+1)-порядка от x, вычисленные в t₀.

Погрешность 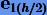решения 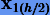, очевидно, будет иметь вид (3.22), но для h/2:

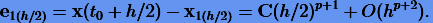(3.23)

Погрешность второго шага состоит из двух частей: из перенесенной погрешности первого шага 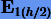и локальной погрешности второго .

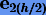Найдем перенесенную погрешность способом, представленном на рис. 3.1а. Составим для нее дифференциальное уравнение. Рассмотрим две одинаковые системы уравнений вида (1.8), но с разными начальными условиями, отличающимися на начальную величину локальной погрешности:

Следовательно, для перенесенной погрешности E = z − x будем иметь дифференциальное уравнение

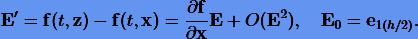
Заметим, что 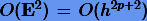— достаточно малая величина, которой здесь можно пренебречь. Решая это уравнение на шаге h/2 методом разложения в ряд Тейлора, получим необходимую перенесенную погрешность, представимую в виде

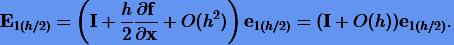(3.24)

Локальная погрешность 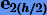на втором шаге будет иметь вид (3.23), но с C, вычисленной при .

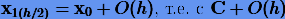Наконец, полная (глобальная) погрешность на втором шаге будет

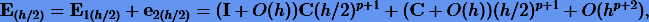
откуда

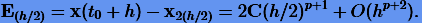(3.25)

Из (3.22) и (3.25) получаем константу C, а затем и погрешность .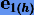

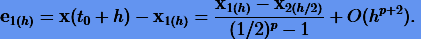(3.26)

Нетрудно видеть, что формула (3.26) позволяет по 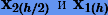получить экстраполяцию численного решения

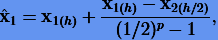(3.27)

лучше представляющее точное решение 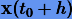. Действительно, согласно (3.26)

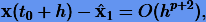
т.е. решение 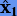(3.27) аппроксимирует точное с порядком p + 1, когда 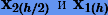— с порядком p.

Таким образом, формула (3.26) дает простой способ оценки погрешности, тогда как (3.27) позволяет дополнительно повысить точность численного интегрирования на один порядок.

Прежде чем переходить к следующему разделу, выведем общую формулу экстраполяции. Рассмотрим два решения , аппроксимирующие точное решение 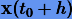и полученные на разных равномерных сетках с шагами h/N и h/M соответственно. Для погрешностей этих решений можно получить оценки, аналогичные (3.25):

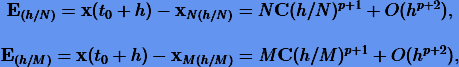
из которых после исключения C будем иметь

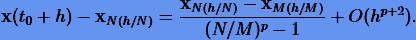
Следовательно, экстраполированное решение порядка p + 1 можно представить в виде

(3.28)

Нетрудно видеть, что (3.27) есть частный случай (3.28) при N = 1 и M = 2.