3.6. Вложенные методы Рунге − Кутты
Вложенные методы Рунге − Кутты основаны на ином способе оценки локальной погрешности 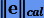 для выбора переменного шага. Их идея состоит в том, чтобы вместо использования экстраполяции Ричардсона построить такие формулы Рунге − Кутты, которые бы кроме основного решения x1 содержали выражения для вспомогательного решения
для выбора переменного шага. Их идея состоит в том, чтобы вместо использования экстраполяции Ричардсона построить такие формулы Рунге − Кутты, которые бы кроме основного решения x1 содержали выражения для вспомогательного решения 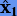 более высокого порядка. Тогда по последнему можно было бы оценить погрешность x1.
более высокого порядка. Тогда по последнему можно было бы оценить погрешность x1.
Следует заметить, что для алгоритма выбора переменного шага можно использовать решение 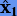 более низкого порядка и по величине его погрешности относительно основного решения x1 выбирать шаг интегрирования. Хотя тогда мы не будем иметь информацию о точности основного решения x1.
более низкого порядка и по величине его погрешности относительно основного решения x1 выбирать шаг интегрирования. Хотя тогда мы не будем иметь информацию о точности основного решения x1.
Вложенные методы Рунге − Кутты имеют табличный вид
В схеме интегрирования основное решение
имеет порядок p, тогда как вспомогательное
— порядок q = p + 1 (либо q = p − 1). При этом ошибка основного решения (либо вспомогательного) оценивается как 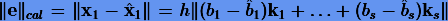 , что дает хорошую оценку главного члена методической погрешности (2.5).
Вложенные методы обычно называют по фамилии автора с указанием порядков основной и вспомогательной схем p (q). На практике широко используются вложенные методы Мерсона, Инглэнда, Фельдберга, а также Дормана − Принса. В качестве примера приведем схему Мерсона 4 (5):
, что дает хорошую оценку главного члена методической погрешности (2.5).
Вложенные методы обычно называют по фамилии автора с указанием порядков основной и вспомогательной схем p (q). На практике широко используются вложенные методы Мерсона, Инглэнда, Фельдберга, а также Дормана − Принса. В качестве примера приведем схему Мерсона 4 (5):
 для выбора переменного шага. Их идея состоит в том, чтобы вместо использования экстраполяции Ричардсона построить такие формулы Рунге − Кутты, которые бы кроме основного решения x1 содержали выражения для вспомогательного решения
для выбора переменного шага. Их идея состоит в том, чтобы вместо использования экстраполяции Ричардсона построить такие формулы Рунге − Кутты, которые бы кроме основного решения x1 содержали выражения для вспомогательного решения 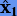 более высокого порядка. Тогда по последнему можно было бы оценить погрешность x1.
более высокого порядка. Тогда по последнему можно было бы оценить погрешность x1.
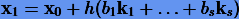
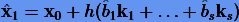
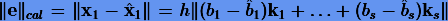 , что дает хорошую оценку главного члена методической погрешности (
, что дает хорошую оценку главного члена методической погрешности (