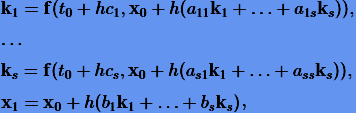
3.7. Неявные методы Рунге − Кутты
Метод
|
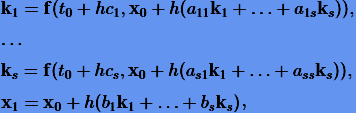(3.33) |
или
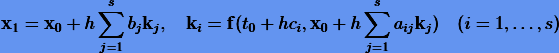
называется s-этапным (s-стадийным) неявным методом Рунге − Кутты для задачи (1.8).
Простые примеры неявных методов Рунге − Кутты — это неявный метод Эйлера (первого порядка)
 |
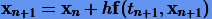(3.34) |
и метод трапеций (второго порядка)
 |
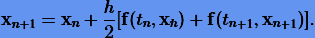(3.35) |
В соответствии с (3.33) неявные методы будут иметь табличный вид
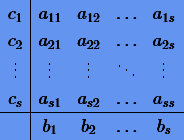
Главным недостатком неявных методов Рунге − Кутты является то, что величины ki задаются в (3.33) неявным образом, и поэтому их нужно находить итерационным способом. Для этого, как правило, используют метод простых итераций:
 |
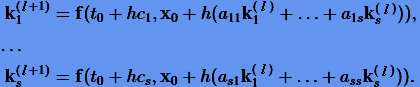(3.36) |
Введем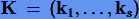 
и норму 
. Тогда (3.36) можно записать в виде 
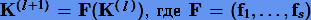, a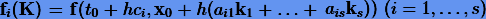 
. Из условия Липшица (1.9) для двух произвольных 
будет справедливо неравенство
 |
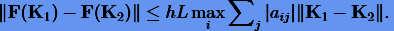(3.37) |
Для сходимости метода простых итераций отображение F должно быть сжимающим, что согласно (3.37) оказывается возможным при условии, когда
 |
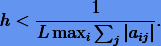(3.38) |
Очевидно, для нахождения ki необходимо, по меньшей мере, две итерации. Отсюда все неявные s-этапные методы требуют вычислений функций f на шаге не меньше, чем 2s. (В данном случае число s и число вычислений функций f не одно и то же, как в явных методах.) Таким образом, неявные методы должны работать медленнее, нежели явные с тем же числом этапов s.
Несмотря на это, привлекательность неявных методов состоит в том, что при всех s существуют такие методы, которые имеют порядок p = 2s. Ж. Кунцман (1961) и Дж. Бутчер (1964) показали, что такой порядок p достигается путем специального выбора коэффициентов ci.
Рассмотрим два метода восьмого-порядка: явный Дормана − Принса (s = 13) и неявный Кунцмана − Бутчера (s = 4). На практике начальные приближения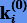 
в неявных методах получают из соответствующих величин на предыдущем шаге. Тогда при хорошем выборе начальных приближений для сходимости итерационного процесса может потребоваться всего 2−3 итерации. Поэтому можно считать, что метод Кунцмана − Бутчера будет вычислять функцию f 8−12 раз на шаге, тогда как метод Дормана − Принса — 13. Следовательно, благодаря своему замечательному свойству неявный метод будет работать быстрее. Кроме того, необходимо заметить, что с повышением порядка p разность s − p для явных методов увеличивается, поэтому указанное преимущество неявных методов будет только возрастать.