3.10. Методы Гаусса

В общем случае метод (3.41) имеет порядок p = s. Однако Бутчер показал, что если коэффициенты b_j и c_j удовлетворяют первым 2s уравнениям во второй системе (3.43) (т.е. если они являются соответственно весами и узлами квадратурной формулы Гаусса), коллокационный метод Рунге − Кутты будет иметь порядок р = 2s.

Известно, что узловые значения квадратурной формулы Гаусса на отрезке [0,1] являются корнями смещенного полинома Лежандра, иначе говоря, они являются решениями уравнения

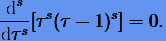(3.45)

Поэтому для получения коллокационного метода порядка р = 2s на практике удобно сначала вычислять c_i из уравнения (3.44), а затем − a_ij и b_i из формул (3.42).

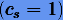Разбиение шага узловыми значениями c_i, удовлетворяющими уравнению (3.44), называется разбиением Гаусса − Лежандра. Если зафиксировать начальное узловое значение , либо конечное , либо и то, и другое 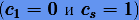, то получим другие известные разбиения Гаусса: левое и правое разбиения Радо и разбиение Лобатто, которые соответственно удовлетворяют уравнениям

Однако любой коллокационный метод, построенный на одном из этих разбиений, будет иметь порядок ниже 2s: узловые значения Радо дают метод порядка р = 2s− 1, а узловые значения Лобатто — р = 2s − 2. Методы, основанные на рассмотренных разбиениях, называют еще методами Гаусса.

Получим метод Кунцмана − Бутчера четвертого порядка (s = 2). Уравнение узлов (3.44) можно преобразовать к виду

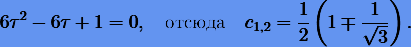
Затем, используя формулы (3.42) с линейными функциям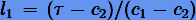и и 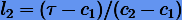, находим коэффициенты

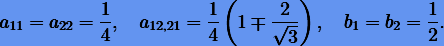
Далее рассмотрим практическую реализацию коллокационных методов на примере интегратора Эверхарта, который широко применяется в небесной механике.