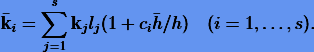3.9. Коллокационные методы

Оказывается, что многие неявные методы Рунге − Кутты некоторым образом эквивалентны так называемым коллокационным методам. Основная идея коллокационных методов для решения обыкновенных дифференциальных уравнений состоит в том, чтобы в качестве приближенного решения x подобрать такой полином 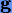порядка s, который бы удовлетворял условиям задачи Коши (1.8) в s + 1 точках:

(3.39)

где c_i — вещественные числа, выбираемые, как правило, на отрезке [0,1]. В соответствии с (3.38) приближенное решение уравнения на шаге h представляется в виде 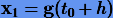. Например, для s = 1 полином должен иметь вид с линейным коэффициентом

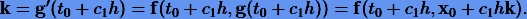
Отсюда видно, что явный и неявный методы Эйлера, а также метод средней точки являются коллокационными с коэффициентами 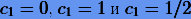соответственно.

Введем обозначение

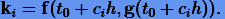(3.40)

Тогда интерполирующая функция Лагранжа для 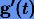будет

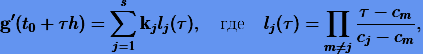(3.41)

а 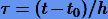. Отсюда интегрируя (3.40) по и пользуясь записью (3.39), будем иметь

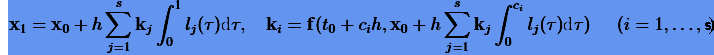(3.42)

(3.41) Нетрудно видеть, что формулы (3.41) совпадают с формулами неявного метода Рунге − Кутты (3.33), где в качестве коэффициентов 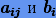выступают

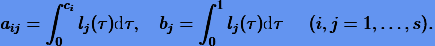(3.43)

Неявные методы Рунге − Кутты с коэффициентами (3.42) называются коллокационными.

Далее поскольку

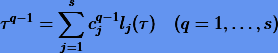
(т.е. интерполяция Лагранжа точна для всех полиномов ниже s-ro порядка), то коэффициенты (3.42) должны удовлетворять системам линейных уравнений

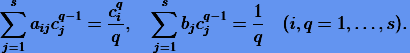(3.44)

Отметим, что коллокационные формулы очень удобны для определения приближенных значений k следующего шага. Обозначая их как , а величину следующего шага 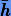, согласно формулам (3.40) получаем экстраполированную оценку