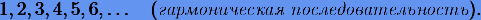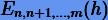 — интерполяционный многочлен порядка m − n с узлами интерполяции
— интерполяционный многочлен порядка m − n с узлами интерполяции  для некоторой функции
для некоторой функции 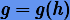 , в частности
, в частности 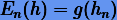 . Тогда справедливы равенства
. Тогда справедливы равенства4.2. Алгоритм Эйткена − Невилла
При p = 1 (метод Эйлера) формулы (4.2) и (4.4) приводят к классической задаче интерполяции. В этом случае для упрощения вычислений интерполяционного многочлена удобно использовать так называемую схему Эйткена − Невилла.
Пусть 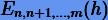 — интерполяционный многочлен порядка m − n с узлами интерполяции
— интерполяционный многочлен порядка m − n с узлами интерполяции  для некоторой функции
для некоторой функции 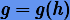 , в частности
, в частности 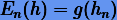 . Тогда справедливы равенства
. Тогда справедливы равенства
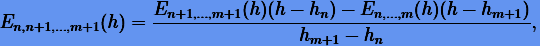 |
(4.5) |
где  — интерполяционный многочлен уже порядка m − n + 1 на сетке
— интерполяционный многочлен уже порядка m − n + 1 на сетке 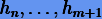 . Фактически, вычисление многочлена
. Фактически, вычисление многочлена 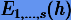 а сетке
а сетке  сводится к последовательному вычислению с помощью (4.5) элементов таблицы
сводится к последовательному вычислению с помощью (4.5) элементов таблицы
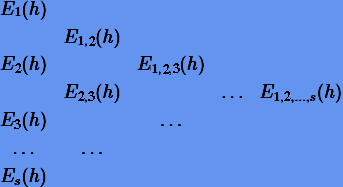 |
(4.6) |
Для экстраполяции нам нужна будет формула (4.5) при h = 0:
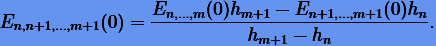 |
(4.7) |
Переобозначим элементы таблицы (4.6) и представим ее как
 |
(4.8) |
Тогда в новых обозначениях формула Эйткена − Невилла (4.7) перепишется в виде
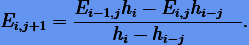 |
(4.9) |
Из (4.9) получаем расчетную формулу для нашей интерполяции
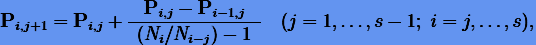 |
(4.10) |
где 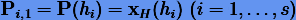 вычисляются по схеме метода Эйлера
вычисляются по схеме метода Эйлера
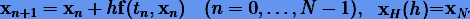
В итоге будем иметь экстраполированное решение 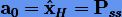 порядка s.
порядка s.
В (4.10) для получения узловых значений в качестве последовательности (4.3) обычно используют
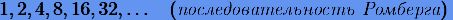
либо