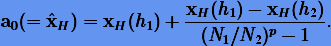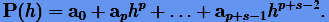
4.1. Общий подход

В соответствии с (4.1) представим интерполяцию приближенного решения в виде многочлена порядка p + s − 2:

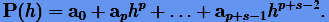(4.2)

Выберем последовательность

(4.3)

и определим соответствующие длины шагов 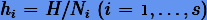. Далее для каждого шага h_i вычислим решение 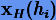каким-либо (опорным) методом Рунге − Кутты порядка p. Тогда, требуя, чтобы 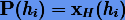, получим следующую систему алгебраических уравнений:

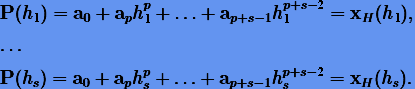(4.4)

После определения из системы (4.4) коэффициентов интерполирующего многочлена нам остается выполнить экстраполяцию при h → 0, что согласно (4.1) и (4.2) дает приближенное решение уже порядка p + s − 1.

При s = 2 интерполяционный многочлен приводится к виду

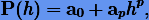
коэффициенты которого будут определяться из системы

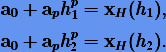
Отсюда получаем экстраполяционную формулу (3.28):