4.3. Метод Грэгга

Метод называется симметричным, если он инвариантен относительно перестановки

Например, неявный метод трапеций — симметричен:

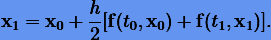
Если опорный метод порядка p = 2q является симметричным, то, как известно, он будет иметь разложение глобальной ошибки по степеням 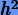, т.е.

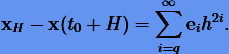
Следовательно, для экстраполяции нужно использовать интерполирующий полином вида

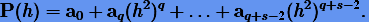(4.11)

Ввиду схожести полиномов (4.11) и (4.2) (при определенном s) вычисление их коэффициентов будет одинаково трудоемко в обоих случаях. Однако примечательно то, что в итоге интерполяция (4.11) дает экстраполированное решение 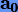порядка 2(q + s − 1) = p + 2s − 2, на s − 1 выше, нежели для (4.2).

У.Б. Грэгг (1963) предложил в качестве опорного использовать симметричный метод второго порядка (p = 2), основанный на правиле средней точки:

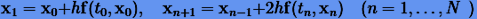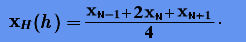(4.12)

Поскольку интерполирующий многочлен (4.11) имеет форму (4.2), для вычисления экстраполяции используется та же формула Эйткена − Невилла, где только h заменяется на 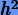, а именно:

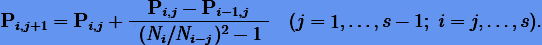(4.13)

Здесь 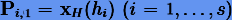получаются из (4.12). При этом последовательности (4.3) выбираются с условием, что 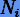должны быть четными. Например,

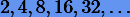
Метод, основанный на (4.12) и (4.13), называется методом Грэгга (или Грэгга − Булирша − Штера). Именно благодаря своим замечательным особенностям он единственный из всех экстраполяционных методов широко используется на практике.