
5.1. Методы Адамса
Многошаговые методы появились гораздо раньше, чем методы Рунге − Кутты. Впервые их получил Дж.К. Адамс еще в 1855 г. Тем же способом, что и Адамс, выведем первое семейство многошаговых методов (Адамса − Башфорта).
Предположим, для задачи Коши (1.8):

нам известны первые r + 1 решения 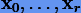 на равномерной сетке
на равномерной сетке  с шагом h. Тогда для шага r + 1 формально решение можно представить как
с шагом h. Тогда для шага r + 1 формально решение можно представить как
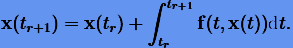 |
(5.1) |
Заменим подынтегральную функцию на ее интерполирующий полином Ньютона, полученнsq по узловым значениям 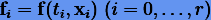 :
:
 |
(5.2) |
где разделенные разности вычисляются из треугольника

Тогда численный аналог (5.1) будет задаваться формулой
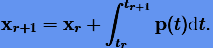 |
(5.3) |
Согласно (5.3) для r = 0, 1, 2 получаем следующие явные формулы Адамса:
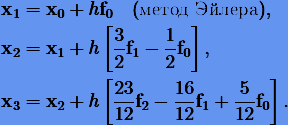
Формулы Адамса получаются при интегрировании интерполяционного многочлена (5.2) от  т.е. вне интервала интерполяции. Однако, как мы знаем, вне этого интервала интерполяционный многочлен обычно дает довольно плохое приближение. Таким образом, явные методы Адамса не очень точны. Чтобы разрешить эту проблему, Адамс предложил для интерполяции использовать значение
т.е. вне интервала интерполяции. Однако, как мы знаем, вне этого интервала интерполяционный многочлен обычно дает довольно плохое приближение. Таким образом, явные методы Адамса не очень точны. Чтобы разрешить эту проблему, Адамс предложил для интерполяции использовать значение 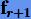 вместо
вместо 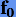 В итоге он получил неявные методы (Адамса − Мультона). Приведем первые из них для r = 0,1:
В итоге он получил неявные методы (Адамса − Мультона). Приведем первые из них для r = 0,1:

Итак, любой s-шаговый метод Адамса можно представить в общем виде
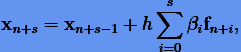 |
(5.4) |
где 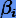 — постоянные метода. Если
— постоянные метода. Если 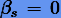 , метод явный, иначе — неявный. Порядок метода определяется точностью интерполирующей формулы (5.2). В общем случае явный метод (5.4) имеет порядок p = s, неявный — p = s + 1.
, метод явный, иначе — неявный. Порядок метода определяется точностью интерполирующей формулы (5.2). В общем случае явный метод (5.4) имеет порядок p = s, неявный — p = s + 1.