5.2. Формулы дифференцирования

Формулы Адамса основаны на приближенном вычислении интеграла в (5.1). Хотя многошаговые методы можно получить иным способом, а именно численно дифференцируя искомое решение.

Интерполяцию Ньютона для x по решениям формально можно представить в виде

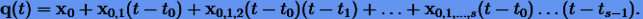(5.5)

Последнее решение x_s пока неизвестно и определим его так, чтобы многочлен q удовлетворял дифференциальному уравнению, по крайней мере, в одной узловой точке:

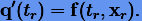(5.6)

Здесь индекс r принимает одно из значений 0, 1, ..., s. После взятия производной в (5.6) и подстановки t_r получаем схему многошагового интегрирования для x_s. Если r = s, метод неявный, иначе — явный. В качестве примера приведем неявный метод для s = 2:

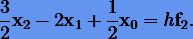
Таким образом, s-шаговый метод, полученный на основе дифференцирования, представим в виде

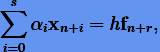(5.7)

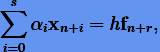
где — постоянные метода. Порядок метода определяется точностью интерполирующей формулы (5.5). В общем случае метод (5.7) имеет порядок p = s.