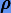 , которая получается после подстановки точного решения в (5.8), является величиной порядка
, которая получается после подстановки точного решения в (5.8), является величиной порядка 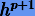 , т.е.
, т.е.5.5. Порядок многошаговых методов
Многошаговый метод (5.8) имеет порядок p, если невязка 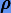 , которая получается после подстановки точного решения в (5.8), является величиной порядка
, которая получается после подстановки точного решения в (5.8), является величиной порядка 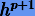 , т.е.
, т.е.
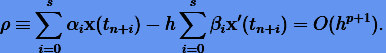 |
(5.9) |
Разложим решения 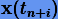 в ряд Тейлора:
в ряд Тейлора:
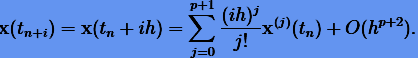 |
(5.10) |
Тогда для производных 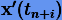 будем иметь
будем иметь
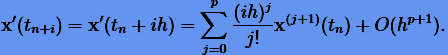 |
(5.11) |
После подстановки (5.10) и (5.11) в (5.9) может быть получено разложение невязки по степеням h:
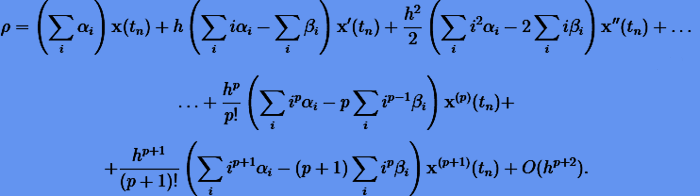 |
(5.12) |
Отсюда для того, чтобы невязка 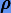 имела порядок
имела порядок 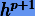 , должны выполняться условия
, должны выполняться условия
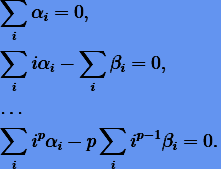 |
(5.13) |
Поскольку 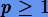 , то первые два условия должны выполняться всегда. Они образуют так называемое условие согласованности.
, то первые два условия должны выполняться всегда. Они образуют так называемое условие согласованности.
Найдем явный двушаговый метод максимально возможного порядка. Явный двушаговый метод можно представить в общем виде
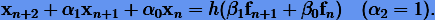
Из (5.13) выпишем первые четыре соотношения:
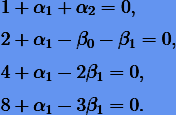
Решая эту систему, получаем 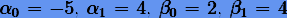 . Пятое соотношение в (5.13):
. Пятое соотношение в (5.13):
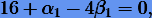
при найденных коэффициентах уже не выполняется. Поэтому двушаговый метод с полученными нами коэффициентами
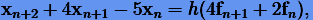 |
(5.14) |
будет иметь третий порядок.