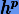5.6. Устойчивость многошаговых методов

Ранее мы выяснили, что глобальная ошибка в методах Рунге − Кутты представляет собой величину порядка .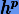

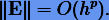
Это означает, что при уменьшении шага интегрирования точность численного решения повышается. Однако для некоторых многошаговых методов это не так, несмотря на то, что согласно условиям (5.13) они имеют малую локальную ошибку (невязку) некоторого порядка h. Для таких методов уменьшение шага интегрирования приводит только к увеличению глобальной ошибки. Эта особенность многошаговых методов связана с понятием неустойчивости.

Важную роль играет поведение решения при h → 0 при фиксированном H = Nh. Очевидно, при h → 0 схема (5.13) приводится к формуле

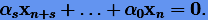(5.15)

Ее можно рассматривать как численную схему, примененную к решению уравнения

Представим решение как и подставим его в (5.15):

Отсюда должно удовлетворять так называемому характеристическому уравнению

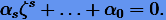(5.16)

Исследование характеристического уравнения усложняется, когда у него имеются кратные корни кратности m. В этом случае т решений для этого корня представляются в виде

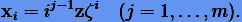(5.17)

Таким образом, если характеристический многочлен (5.16) имеет корни кратностей 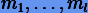соответственно, то суперпозиция решений (5.17) будет давать общее решение уравнения:

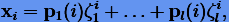(5.18)

где 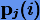— многочлены степеней 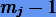, коэффициенты которых определяются из начальных условий. Поэтому для ограниченности решений x_i необходимо потребовать, чтобы, во-первых, корни 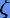лежали внутри единичной окружности , и, во-вторых, чтобы все корни на единичной окружности 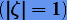были простыми. Многошаговые методы, удовлетворяющие этим требованиям, называются устойчивыми по Далквисту или D-устойчивыми.

Исследуем на устойчивость метод (5.14). Характеристический многочлен для него запишется как

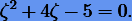
Его корни 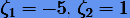. Корень , поэтому метод (5.14) неустойчив

Наконец, в дополнение к данному разделу отметим известный факт по поводу абсолютной устойчивости многошаговых методов. Доказано, что среди линейных многошаговых методов нет явных А-устойчивых, а порядок неявных А-устойчивых методов не превышает двух.