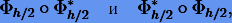
6.4.3. Методы Штермера − Верлета

Скомпануем две схемы интегрирования как

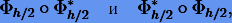
где в качестве Φ выберем первую симплектическую схему Эйлера (6.15). Тогда составные схемы будут

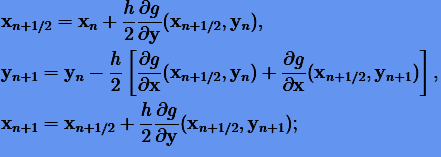(6.18)

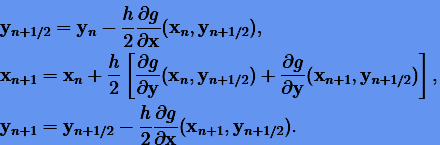(6.19)

Методы, определяемые схемами (6.18) и (6.19), называются методами Штермера − Верлета.

Для важного в классической механике случая 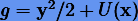схемы перепишутся как

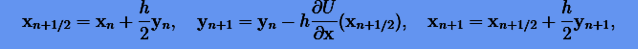(6.20)

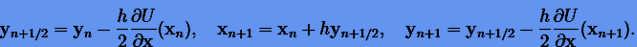(6.21)

Совокупность формул интегрирования (6.20) образует так называемую "схему прыгающей лягушки". Если вторую схему (6.21) записать для двух шагов, то удается исключить переменные y и в результате можно получить многошаговую схему

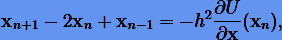
которая применялась еще И. Ньютоном, Ж.Л. Даламбером и Й.Ф. Энке.

Отметим важные свойства методов Штермера − Верлета: 1) методы имеют второй порядок; 2) они симплектические и симметрические; 3) для разделенного гамильтониана 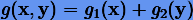методы явные. Таким образом, методы Штермера − Верлета геометрические, однако для долгосрочного интегрирования в задачах динамической астрономии они в оригинальном виде не востребованы, поскольку имеют низкий порядок. Тем не менее эти методы могут быть весьма полезными для получения составных геометрических методов высоких порядков.