6.4. Симплектические и симметрические методы

6.4.1. Простые симплектические методы

Симплектические схемы интегрирования строятся таким образом, чтобы отображение

было каноническим. Тогда должна существовать производящая функция, например, 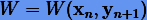такая, что

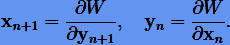
Выберем в качестве таких функций

тогда получаем симплектические схемы интегрирования первого порядка

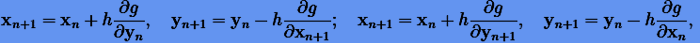(6.15)

в которых без труда узнаем первую и вторую симплектические схемы Эйлера (6.11) в случае интегрирования уравнений гармонического осциллятора, если вместо g подставить (6.6).

Для метода второго порядка выберем

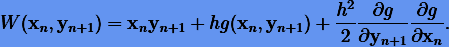
Тогда данной производящей функции будет соответствовать неявный метод

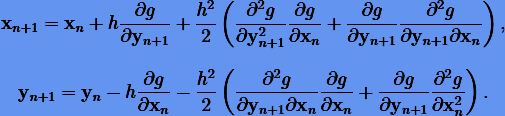
Методы более высоких порядков можно конструировать подобным образом. Однако очевидно, что такой подход не столь эффективен, поскольку требует получения формул для вычисления частных производных высоких порядков от гамильтониана канонической системы.