Приложение
Kepler_Solver

Флэш-проект Kepler_Solver предназначен для демонстрации эффективности численных методов интегрирования применительно к плоской задаче двух тел. В проекте программно реализованы две группы методов низких порядков: Рунге-Кутты (Эйлера, Хойна и классический) и симплектические (Эйлера и Штермера-Верлета второго порядка). В каждом методе имеется возможность коррекции решения за его отклонения от энергетической гиперповерхности (метод Накози), что при численном интегрировании позволяет сохранять интеграл энергии, а это, в свою очередь, улучшает поведение ошибки интегрирования. Все методы работают в двух режимах: постоянного, либо переменного шага. Переменный шаг выбирается пропорционально радиус-вектору. Условия задачи определяются эксцентриситетом орбиты, задаваемым пользователем.
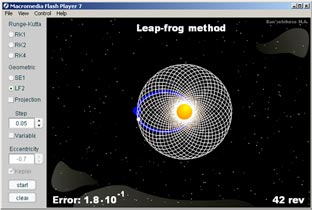
Демонстрационная часть флэш-проекта представляет собой панель управления и поле визуализации результатов интегрирования. На панели управления: RK1 − метод Эйлера (первого порядка); RK2 − метод Хойна и трапеций (второго порядка); RK4 − классический метод Рунге-Кутты и метод Гаусса (четвертого порядка); Iterations − выбор явного (Exp.) либо неявного (2-8) метода (количество итераций для решения нелинейной системы); SE1 − симплектический метод Эйлера (первого порядка); LF2 − метод прыгающей лягушки или Штермера-Верлета (второго порядка); Projection − коррекция Накози; Step − выбор шага от 0.01 до 1; Variable − режим переменного шага; Eccentricity − эксцентриситет от -0.9 до 0.9; Kepler − визуализация точной орбиты; Start/Stop − запуск и остановка интегрирования; Clear − инициализация задачи. Все кнопки управления (кроме Eccentricity и Kepler) также остаются доступными в процессе интегрирования. На поле визуализации результатов интегрирования: белой (синей) точкой и линией представляется соответственно вычисляемые (точные) положение объекта и орбита; вверху указан метод, которым интегрируется орбита; внизу дается ошибка в вычисляемом векторе положения и число оборотов объекта (на точной орбите).
Интегратор Гаусса − Эверхарта
Версия курса для печати
Численные методы интегрирования ОДУ
Замечание: Если файл не открывается, нажмите на нем правой клавишей мыши и выберите из списка "Сохранить по ссылке как ...".