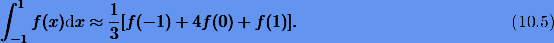10.2 Метод неопределенных коэффициентов
Допустим, по n узловых точек строится квадратурная формула
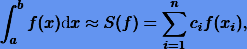
точная для многочленов наиболее высокой степени. Погрешность квадратуры будет
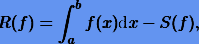
тогда при
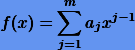
имеем
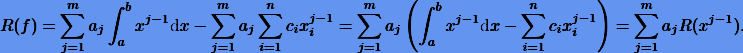
Таким образом, нужно добиться выполнения равенств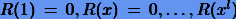 
при возможно большем значении l. В итоге получаем систему уравнений для коэффициентов ci
Построим квадратурную формулу для интеграла
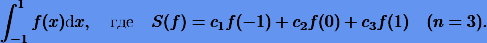
В этом случае система (10.4) перепишется как
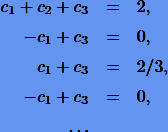
Поскольку нужно определить 3 коэффициента, то, вообще говоря, можно решить лишь первые три уравнения, из которых получаем
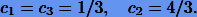
Заметим, что при полученных коэффициентах четвертое уравнение выполняется автоматически. Таким образом, мы получили квадратуру, точную для многочленов третьей степени, называемую формулой Симпсона:
