ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ

10.4 Квадратурные формулы Ньютона-Котеса

Квадратурные формулы Ньютона-Котеса получаются с помощью интегрирования интерполяционных многочленов.

Интеграл вида (10.1) с произвольными пределами a и b можно выразить через интеграл с фиксированными пределами —1 и 1. Действительно, применяя преобразование

будем иметь

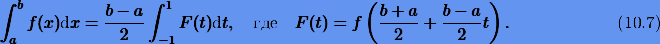
Заменяя функцию F(t) интерполяционным полиномом Лагранжа 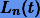(7.5), построенный на сетке , получим следующие квадратурные формулы

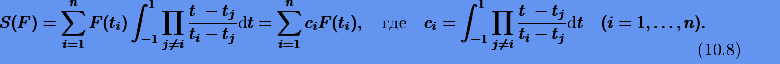
Тогда согласно (10.7) квадратура для интеграла (10.1) будет

где x_i соответствуют узлам t_i по формуле (10.6).

Следует заметить, что при наличии в интеграле (10.7) весовой функции p(x) коэффициенты c_i (10.8) будут вычисляться как

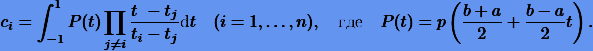
Выведем некоторые формулы Ньютона-Котеса с единичной весовой функцией для равномерной сетки . При линейной интерполяции функции f(x) (n = 2) будем иметь квадратуру

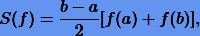
в которой мы без труда узнаем формулу трапеций (10.3). При n = 3 фактически получаем формулу Симпсона (10.5), записанную для произвольных пределов a и b:

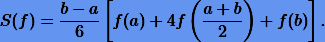
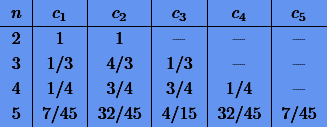
Наконец, составим таблицу коэффициентов c_i для равномерной сетки до n = 5:

Оценим погрешность формул Ньютона-Котеса. Поскольку квадратуры в данном случае получаются путем замены подынтегральной функции, то погрешность может быть представлена в виде

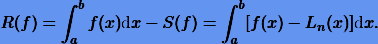
Согласно (7.6) справедлива оценка

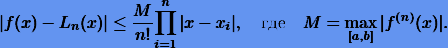
Тогда

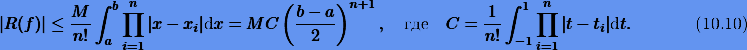
где

Отсюда моЖно полагать, что при уменьшении отрезка [a, b] погрешность квадратуры будет вести себя пропорционально величине 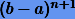.