10.5 Повышение точности численного интегрирования
10.5.1 Квадратурные формулы Гаусса
Особенность рассматриваемых ранее квадратур состоит в том, что они строились на заданной равномерной сетке, для которой в общем случае удается получить квадратуры, точные для всех многочленов степени n — 1. Хотя точность квадратурных формул можно повысить, если узловые значения включить в набор определяемых коэффициентов.
Поставим задачу определить 2n коэффициентов 
, которые бы удовлетворяли системе (уже нелинейных) уравнений (10.4). Очевидно, это оказывается возможным для первых 2n уравнений. Вычислив эти коэффициенты, мы фактически получим квадратуры, точные для многочленов порядка 2n — 1. Такие квадратуры называются формулами Гаусса.
Получим некоторые простые квадратуры Гаусса до n = 3. Для n = 1 будем иметь простую систему с двумя неизвестными, которая дает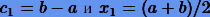 
. В итоге получаем формулу среднего прямоугольника, точную для линейных функций:
Для n = 2 найдем коэффициенты применительно к интегралам с пределами —1 и 1. Система (10.4) в этом случае примет вид
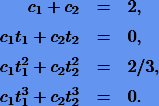
После несложных манипуляций находим коэффициенты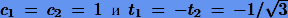 
. Тогда согласно (10.7) применительно к интегралам с произвольными пределами a и b получаем квадратуру, точную для полиномов третьей степени:
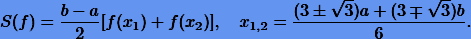
Нахождение гауссовой квадратуры для n = 3 более трудоемко, поэтому мы не будем выводить ее, а просто запишем уже известные коэффициенты:
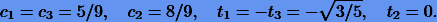
В связи с тем, что для больших п нахождение коэффициентов представляет собой довольно утоми¬тельное занятие, на практике их вычисляют иначе. Оказывается, что узловые значения ti гауссовых квадратур являются корнями так называемых полиномов Лежандра, т.е. удовлетворяют уравнению
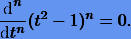
Поэтому сначала определяют корни полинома Лежандра, а затем, пользуясь соотношениями (10.8), находят коэффициенты ci.